Компрессора. Исследование движения механизма

3.1 Построение планов механизмов, индикаторных диаграмм и нахождение сил для расчётного положения действующих на звенья механизма

Выполняем построение планов механизма и кинематическую схему в масштабе m_l = 0,002 м/мм, плана скоростей в масштабе m_v = 0,25 м × с^-1/мм, плана ускорений в масштабе m_а =40 м × с^-2/мм и индикаторную диаграмму двигателя.

По индикаторной диаграмме определяется удельное давление на поршень в каждом положении механизма. Проводя из каждого положения прямые параллельные оси Р получим на диаграмме разметку положений точек D и С. При нумерации положений следует учитывать, что порядок положений на диаграмме должен соответствовать направлению рабочего и холостого хода ползуна.

Масштаб индикаторной диаграммы по оси Р:

где Р_mах - максимальное удельное давление на поршень, равное 5 МПа;

h - принятая высота диаграммы, равная 62.5 мм.

Сила давления газа на поршень:

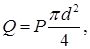
где Р - удельное давление газа на поршень в Па (1 Па=1 Н/м);

d - диаметр поршня в м.

Найдём значения сил для расчётного 7 положения.

Вычислим силы давления газа на поршень. Удельное давление газа на поршень определяется по формуле:

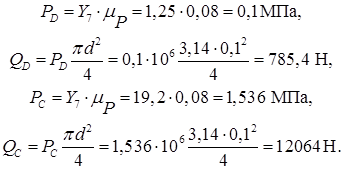
Силы тяжести приложены к центрам массы звеньев. Они вычисляются по формуле:

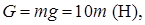
где m - масса звена в кг.

Найдём значения сил тяжести для каждого звена:

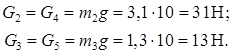
Силы инерции определяются по формуле:

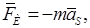
где а_s - ускорение центра масс звена в м/с².

Направление сил инерции F_И противоположно направлению векторов ускорения центра масс звена. Для первого звена сила инерции равна 0, так как центр масс звена лежит на оси его вращения и его ускорение равно нулю. Найдём силу инерции для остальных звеньев:

Момент сил инерции (инерционные моменты) звеньев определяются по формуле:

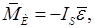
где ε - угловое ускорение звена в рад/с²;

Js - момент инерции масс звеньев относительно оси, проходящей через центр масс перпендикулярно к плоскости движения, кг × м².

Дата добавления: 2015-10-13