Прохождение звука через слой (среда II) между двумя различными средами (I и III)

Вывод формул для этого случая проводится по ранее изложенному методу. Для нормального падения звука (θ1 = 0) коэффициент звукоизоляции

где R1 = р1c1, R2 = p2c2 и R3 = p3c3 — акустические сопротивления сред I, II и III. Эта формула может быть применена и для твердых тел. Когда k2d<1 и λ2 > d, а также k2d≈πn, т. е. sin k2d≈0, получим:

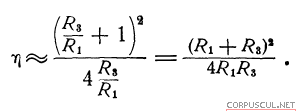
Это соотношение совпадает с равенством (3,5) для случая прохождения через границу двух сред. Таким образом, для очень тонких слоев или очень низких частот, а также при условии звукоизоляция не зависит от свойств промежуточного слоя. Если sin k2d≠0, то присутствие промежуточного слоя увеличивает звукоизоляцию, когда R2 лежит по величине между R1 и R3, если этого нет, то наличие слоя уменьшает звукоизоляцию. Если sink2d = 1, т.е.

Из формулы (3,29) видно, что если R2 лежит между R1 и R3, то соотношение (3,30) выражает минимум звукоизоляции; если 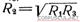то η= 1, т. е. звукоизоляции нет.
Условие d=(n + 0.5)(λ/2) для минимума звукоизоляции, т. е. для наибольшей звукопрозрачности, аналогично условию, применяемому в оптике для расчета „просветляющих" слоев. Для иллюстрации применения „просветляющиха слоев в акустике рассмотрим случай прохождения звука из воды в воздух, при котором просветляющий слой должен иметь Вещества, обладающие таким акустическим сопротивлением, найти невозможно. Однако можно искусственно создать такой материал, используя резину с воздушными пузырьками. Нетрудно видеть, что если из общего объема (V1 + V2) часть V2 заполнена воздухом, а часть V1 относится к резине, то модуль объемной упругости такого сложного материала

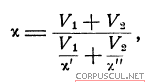
где х' и х"— модули объемной упругости..соответственно резины и воздуха (для резины модуль примерно такой же, как и для воды, т. е. 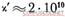для воздуха при звуковых колебаниях ).
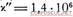Плотность сложного материала будет достаточно точно равна 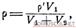где р' ≈ 1,1—плотность резины. Для квадрата акустического сопротивления слоя получим:

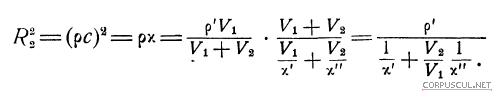
Приравнивая эту величину значению 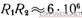получим V1 / V2 ≈ 1 / 2.55 что соответствует 27% содержания пузырьков воздуха в общем объеме.

20 Что такое поглощение звука?

Поглощение звука, превращение энергии звуковой волны в другие виды энергии, и в частности в тепло; характеризуется коэффициентом поглощения а, который определяется как величина, обратная расстоянию, на котором амплитуда звуковой волны уменьшается в е = 2,718 раз. а выражается в см^-1 т. е. в неперах на см или же в децибелах на м (1 дб/м = 1,15×10^-3 см^-1). П. з. характеризуют также коэффициент потерь e = al/p: (где l — длина волны звука) или добротностью Q =1/e. Величина al называется логарифмическим декрементом затухания. При распространении звука в среде обладающей вязкостью и теплопроводностью,

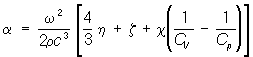, (1)

где r — плотность среды, с — скорость звука в ней, w — круговая частота звуковой волны, h и x — коэффициент сдвиговой и объёмной вязкости соответственно, c — коэффициент теплопроводности, С_р и C_v— теплоёмкости среды при постоянном давлении и объёме соответственно. Если ни один из коэффициентов h, x и c не зависит от частоты, что часто выполняется на практике, то a ~ w². Если при прохождении звука нарушается равновесное состояние среды, П. з. оказывается значительно большим, чем определяемое по формуле (1). Такое П. з. называется релаксационным (см. Релаксация) и описывается формулой

,

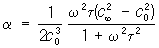где t — время релаксации, c ₀ и c _¥— скорости звука при wt << 1 и при wt > 1 соответственно. В этом случае П. з. сопровождается дисперсией звука. Величина a /f², где f = w/2p, является характеристикой вещества, определяющей П. з. Она, как правило, в жидкостях меньше, чем в газах, а в твёрдых телах для продольных волн меньше, чем в жидкостях.

П. з. в газах зависит от давления газа, разрежение газа эквивалентно увеличению частоты. Теплопроводность и сдвиговая вязкость в газах дают в П. з. вклад одного порядка величины. В жидкостях П. з. в основном определяется вязкостью, а вклад теплопроводности пренебрежимо мал. В большинстве жидкостей для П. з. существенны объёмная вязкость и релаксационные процессы. Частота релаксации в жидкостях, т. е. величина w _р =1/t, как правило, очень велика и область релаксации оказывается лежащей в диапазоне высоких ультразвуковых и гиперзвуковых частот. Коэффициент П. з. обычно сильно зависит от температуры и от наличия примесей.

П. з. в твёрдых телах определяется в основном внутренним трением и теплопроводностью среды, а на высоких частотах и при низких температурах — различными процессами взаимодействия звука с внутренними возбуждениями в твёрдом теле, такими, как фононы, электроны, спиновые волны и пр. Величина П. з. в твёрдом теле зависит от кристаллического состояния вещества (в монокристаллах П. з. обычно меньше, чем в поликристаллах), от наличия дефектов, примесей и дислокаций, от предварительной обработки, которой был подвергнут материал. В металлах, подвергнутых предварительной термообработке, а также ковке, прокатке и т.п., П. з. часто зависит от амплитуды звука. Во многих твёрдых телах при не очень высоких частотах a ~ w, поэтому величина добротности не зависит от частоты и может служить характеристикой потерь материала. Самое малое П. з. при комнатных температурах было обнаружено в некоторых диэлектриках, например в топазе, берилле, железоиттриевом гранате (a ~ 15 дб/см при f =9 Ггц). В металлах и полупроводниках П. з. всегда больше, чем в диэлектриках, поскольку имеется дополнительное поглощение, связанное с взаимодействием звука с электронами проводимости. В полупроводниках это взаимодействие при определённых условиях может приводить к "отрицательному поглощению", т. е. к усилению звука (см. Усиление ультразвука). С ростом температуры П. з., как правило, увеличивается.

Наличие неоднородностей в среде приводит к увеличению П. з. В различных пористых и волокнистых веществах П. з. велико, что позволяет применять их для заглушения и звукоизоляции.

21 В чем суть дифракции звука и где она проявляется на практике?

Дифракция (от лат. diffractus - разломанный) волн, явления, наблюдаемые при прохождении волн мимо края препятствия, связанные с отклонением волн от прямолинейного распространения при взаимодействии с препятствием. Из-за Дифракция волны огибают препятствия, проникая в область геометрической тени. Именно Дифракция звуковых волн объясняется возможность слышать голос человека, находящегося за углом дома. Дифракцией радиоволн вокруг поверхности Земли объясняется приём радиосигналов в диапазоне длинных и средних радиоволн далеко за пределами прямой видимости излучающей антенны.

Дифракция волн - характерная особенность распространения волн независимо от их природы. Объяснить Дифракция в первом приближении можно, применив Гюйгенса - Френеля принцип. Согласно этому принципу, рассматривая распространение какой-либо волны, можно каждую точку среды, которой достигла эта волна, считать источником вторичных волн. Поэтому, поставив на пути волн экран с малым отверстием (диаметр порядка длины волны), получим в отверстии экрана источник вторичных волн, от которого распространяется сферическая волна, попадая и в область геометрической тени. Если имеется экран с двумя малыми отверстиями или щелями, дифрагирующие волны накладываются друг на друга и в результате интерференции волн дают чередующееся в пространстве распределение максимумов и минимумов амплитуды результирующей волны с плавными переходами от одного к другому. С увеличением количества щелей максимумы становятся более узкими. При большом количестве равноотстоящих щелей (дифракционная решётка) получают резко разделённые направления взаимного усиления волн.

Дифракция волн существенно зависит от соотношения между длиной волны l и размером объекта, вызывающего Дифракция Наиболее отчётливо Дифракция обнаруживается в тех случаях, когда размер огибаемых препятствий соизмерим с длиной волны. Поэтому легко наблюдается Дифракция звуковых, сейсмических и радиоволн, для которых это условие обычно всегда выполняется (l ~ от м до км), и гораздо труднее наблюдать без специальных устройств дифракцию света (l ~ 400-750 нм). Эта же причина приводит к многим техническим трудностям при изучении волновых свойств др. объектов. Так, поскольку рентгеновские лучи имеют длину волны от сотен до 0,0001 А, дифракционную решётку с таким расстоянием между щелями изготовить невозможно, поэтому немецкий физик М. Лауэ для изучения дифракции рентгеновских лучей использовал в качестве дифракционной решётки кристалл, в котором атомы (ионы) расположены в правильном порядке.

Дифракция волн сыграла большую роль в изучении природы микрочастиц. Экспериментально было установлено, что при прохождении микрочастиц (например, электронов) через среду (газ, кристалл) наблюдается Дифракция Дифракция частиц является следствием того, что микрочастицы обладают двойственной природой (так называемым корпускулярно-волновым дуализмом): в одних явлениях поведение микрочастиц может быть объяснено на основе представления о частицах, в других, как, например, в явлениях Дифракция, на основе представления о волнах. Согласно квантовой механике, каждой частице соответствует так называемая волна де Бройля, длина которой зависит от энергии частицы. Так, электрону с энергией 1 эв соответствует волна де Бройля длиной того же порядка, что и размер атома. Дифракция электронов и нейтронов широко пользуются для изучения строения вещества.

Дата добавления: 2015-09-05