Приведите выражение для определения скорости звука.

Скорость звука в однородной жидкости (или газе) вычисляется по формуле:

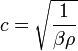
где 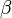— адиабатическая сжимаемость среды; 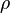— плотность.

Для газов эта формула выглядит так:

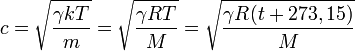
где 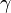— показатель адиабаты: 5/3 для одноатомных газов, 7/5 для двухатомных (и для воздуха), 4/3 для многоатомных; 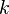— постоянная Больцмана; 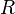— универсальная газовая постоянная; 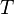— абсолютная температура в кельвинах; 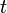— температура в градусах Цельсия; 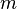— молекулярная масса; 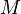— молярная масса. По порядку величины скорость звука в газах близка к средней скорости теплового движения молекул и в приближении постоянства показателя адиабаты пропорциональна квадратному корню из абсолютной температуры.

Данные выражения являются приближенными, поскольку основываются на уравнениях, описывающих поведениеидеального газа. При больших давлениях и температурах необходимо вносить соответствующие поправки.

Для расчета сжимаемости многокомпонентной смеси, состоящей из невзаимодействующих друг с другом жидкостей и/или газов, применяется уравнение Вуда. Это же уравнение применимо и для оценки скорости звука в нейтральных взвесях.

Для растворов и других сложных физико-химических систем (например, природный газ, нефть) данные выражения могут давать очень большую погрешность.

[править]Твёрдые тела

В однородных твёрдых телах могут существовать два типа объемных волн, отличающихся друг от друга поляризацией колебаний относительно направления распространения волны: продольная (P-волна) и поперечная (S-волна). Скорость распространения первой 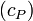всегда выше, чем скорость второй :

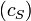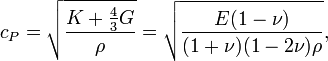
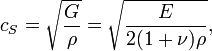
где 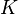— модуль всестороннего сжатия; 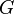— модуль сдвига; 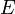— модуль Юнга; 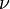— коэффициент Пуассона. Как и для случая с жидкой или газообразной средой, при расчетах должны использоваться адиабатические модули упругости.

В многофазных средах из-за явлений неупругого поглощения энергии скорость звука, вообще говоря, зависит от частоты колебаний (то есть наблюдается дисперсия скорости). Например, оценка скорости упругих волн в двухфазной пористой среде может быть выполнена с применением уравнений теории Био-Николаевского. При достаточно высоких частотах (выше частоты Био) в такой среде возникают не только продольные и поперечные волны, но также и продольная волна II-рода. При частоте колебаний ниже частоты Био, скорость упругих волн может быть приблизительно оценена с использованием гораздо более простых уравнений Гассмана.

При наличии границ раздела, упругая энергия может передаваться посредством поверхностных волн различных типов, скорость которых отличается от скорости продольных и поперечных волн. Энергия этих колебаний может во много раз превосходить энергию объемных волн.

[править]Скорость звука в воде

В чистой воде скорость звука составляет 1500 м/с (см. опыт Колладона—Штурма). Прикладное значение имеет также скорость звука в солёной воде океана. Скорость звука увеличивается в более солёной и более тёплой воде. При большем давлении скорость также возрастает, то есть чем глубже, тем скорость звука больше. Разработано несколько теорий распространения звука в воде.

Например, теория Вильсона 1960 года для нулевой глубины даёт следующее значение скорости звука:

,

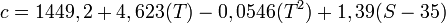где c — скорость звука в метрах в секунду, T — температура в градусах Цельсия, S — солёность в промилле.

Иногда также пользуются упрощённой формулой Лероя:

,

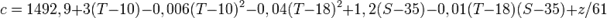где z — глубина в метрах. Эта формула обеспечивает точность порядка 0,1 м/с для T < 20 °C и z < 8 000 м.

При температуре 24 °C, солёности 35 промилле и нулевой глубине, скорость звука равна около 1 532,3 м/c. При T = 4 °C, глубине 100 м и той же солёности скорость звука равна 1 468,5 м/с^[2].

Дата добавления: 2015-09-05