Отражение от абсолютно твердой плоской поверхности при наклонном падении звука.

Пусть волна, падающая слева (рис) на абсолютно твердую поверхность под углом θ, за некоторый промежуток времени распространяется на отрезок АО = S.

Длину отрезка можно выразить через координаты х,у точки А:

Величина S играет теперь в уравнении волны роль фазового пути, которую раньше, например в формуле (3,1), играла координата х, причем за положительное направление S принято направление распространения волны. Для падающей волны потенциал скоростей будет:

Аналогично для отраженной волны отрезок ОА' по ходу волны равен S' = — х соs θ' —у sin θ', где θ' — угол отражения, и потенциал скорости будет равен:

Сумма Ф1 и Ф'1 двух решений (3,7) и (3,8) должна удовлетворять линейному дифференциальному уравнению волны, что следует из принципа суперпозиции. На границе (при х = 0) должно быть соблюдено при любых у равенство нулю нормальной компоненты скорости:

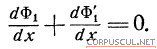
Этому условию мы удовлетворим, приняв

Следовательно, амплитуда отраженной волны равна амплитуде падающей и угол отражения равен углу падения. Итак, для потенциала скоростей получим:

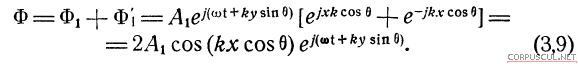
В этом выражении множитель характеризует волну, бегущую вдоль оси у в отрицательном направлении (т. е. вниз — на рис). Скорость этого следа волны найдем из соотношения с'= w / (k sinθ), так как волновое число в данном случае равно k sinθ. Следовательно,

Из формулы ясно, что фазовая скорость следа волны больше, чем скорость звука с. Множитель соs (kxсоsθ) в уравнении (3,9), зависящий только от х, показывает, что амплитуда волны испытывает периодические изменения по направлению оси х. Таким образом, волна, бегущая вдоль оси у, «модулирована» в пространстве по закону соs (kx соsθ). В плоскостях, перпендикулярных оси х, амплитуда имеет везде одинаковое значение. Плоскость максимальных амплитуд мы получим, полагая кxсоsθ = nπ. Расстояние между плоскостями максимальной амплитуды будет больше полуволны. Таким образом, параллельно отражающей поверхности образуются интерференционные полосы
с расстояниями между пучностями и узлами, равными (рис.). Эти волны можно назвать „псевдостоячими". Параллельно отражающей поверхности, как уже сказано, бежит волна со скоростью
равной формуле 3.10, модулированная по фронту. Поток энергии в этой волне направлен параллельно оси у, т. е. вдоль границы. Если θ = 0 (нормальное падение), то из уравнения (3.9) получим:

В этом случае волна вдоль поверхности исчезает, и мы имеем процесс обычных стоячих волн с узловыми плоскостями, отстоящими на λ / 2 друг от друга. Стоячая волна характеризуется выражением, в котором переменные х и t входят раздельно в двух множителях. Важно отметить, что при θ = 0 скорость следа волны (3,10) равна бесконечности, поток же энергии вдоль стенки равен при этом нулю.

Совершенно такой же процесс, как при отражении под углом, мы получим при наложении двух плоских волн одинаковой амплитуды, идущих под углом друг к другу. Пусть волны идут в направлениях АА' и ВВ' лежащих под углом 180° — 2θ (првый рис.). Перпендикулярно оси у везде скорость частиц будет равна нулю, так как ввиду симметрии ^-компоненты скорости в двух составляющих волнах будут равны и противоположны друг другу. Аналогичная картина волн, соответствующая отражению от стенки с другой стороны, будет иметь место и в правом полупространстве х' > 0. Картина отражения плоской волны АО от абсолютно твердой поверхности может быть, таким образом, формально представлена как наложение на прямую волну АА' ее „зеркального" отражения в плоскости Y = 0, т. е. волны ВВ'.

Пусть границей раздела двух сред является плоскость Х = 0 (на ниж. рис.) и на эту границу раздела падает под углом θ1 плоская волна.

В первой среде возникает плоская, отраженная под углом θ1 волна; во второй среде возникает преломленная под углом θ2 волна. Удельное акустическое сопротивление первой среды обозначим через R1=p1c1, второй - R2=p2c2. Напишем отдельно волновые уравнения для каждой среды:

Давления и нормальные компоненты скорости на границе раздела с обеих сторон должны быть одинаковы. Поэтому граничные условия могут быть записаны так:

Потенциалы скоростей в I и II средах можно представить в виде:

Легко показать, что b1 = b2 = b. Действительно, скорости движения следа волны вдоль оси у в I и II средах, равные соответственно w / b1 и w / b2, должны быть равны. В самом деле,
если вдоль границы с левой стороны движется максимум или минимум давления, то в силу непрерывности давления с правой стороны, параллельно ему, также должен двигаться максимум или минимум давления, равный по величине и с той же скоростью. Таким образом,

Мы получили закон Снеллиуса, который соблюдается не только для звука, но и для любых волновых процессов. Подставляя в граничные условия (3, 13) выражения (3, 14), получим:

Из этой системы уравнений можно определить отношения амплитуд:

Из этих формул при одинаковых плотностях двух сред (р1 = р2) после некоторых преобразований найдем:

Формулы (3,18) и (3,19) совпадают с формулами Френеля для коэффициента отражения света, поляризованного соответственно параллельно или перпендикулярно плоскости падения.
Подставляя а1 и а2 в уравнение (3,17) и используя закон преломления, получим:

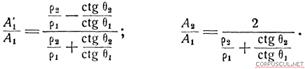
Коэффициент отражения и коэффициент проникновения волны давления найдем, учитывая, что р = jwpФ:

Принимая во внимание, что на основании (3,14) амплитуды потенциалов скоростей связаны с соответствующими амплитудами Q скорости частиц соотношениями 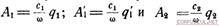определим коэффициент отражения rq и коэффициент проникновения tq волны скорости частиц:

Из формулы (3,17) следует, что отраженной волны не будет при условии:

Учитывая закон преломления, получим:

Если 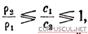то ctg θ1 будет положителен и может быть найден некоторый угол θ1 в пределах от 0 до 90°, при котором отсутствует отражение звука на границе двух сред. Например, для этилового спирта р1 = 0,79; и и для хлороформа р2 = 1,49 и Для этих сред из уравнения (3,21) следует, что

Если скорость звука во второй среде гораздо меньше, чем в первой (с1 < с2) то sinθ2 ≈ 0 и θ2 ≈ 0. Таким образом, вторая среда может пропускать волны только в направлении нормали к границе раздела. Таким свойством обладает, например, модель, состоящая из тонких капилляров, перпендикулярных к границе раздела (модель Рэлея). При этих условиях

Вообще говоря, в этих случаях удельное сопротивление второй среды может быть комплексным и характеризоваться некоторым нормальным импедансом Z2 (таким свойством обладают, например, многие пористые звукопоглощающие материалы применяемые в архитектурной акустике). Если среду, на которую падает звук, можно характеризовать нормальным импедансом Z2 то коэффициент отражения

Дата добавления: 2015-09-05