Приведите комплексную запись давления звуковой волны.

Для поля гармонического во времени, используя комплексное представление, волновое уравнение (1.11) примет более простой вид:

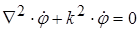(1.18)

где 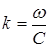- волновое число, постоянная распространения.

Уравнение (1.18) называется уравнением Гельмгольца. Всякое решение уравнения Гельмгольца представляет собой распространяющуюся гармоническую волну. Поверхность, на которой колебания частиц происходят в фазе, называется фронтом волны. По форме фронта (сфера, цилиндр, плоскость) волны называются сферическими, цилиндрическими, плоскими.

Для плоской гармонической волны, распространяющейся, например вдоль оси x, уравнение (1.18) принимает вид:

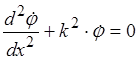, (1.19)

а его решение с учетом временного множителя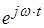

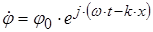
Если плоская гармоническая волна распространяется в произвольном направлении 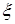, то тогда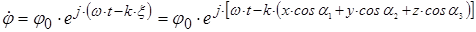

где 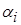- углы между направлением 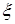и положительными осями .

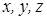По известному потенциалу

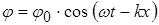
вычислим колебательную скорость и акустическое давление

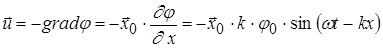(1.20)

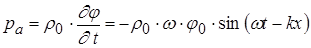(1.21)

В бегущей волне колебательная скорость имеет одну компоненту 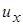, это значит, что частицы среды в волне колеблются в направлении ее распространения, т.е. акустическая волна является продольной. Согласно (1.20), (1.21) акустическое давление и колебательная скорость прямо пропорциональны частоте.

Проведем аналогию акустических величин с электрическими. И хотя эта аналогия формальна, поскольку природа механических и электрических явлений различна, но в ряде случаев использование этой аналогии оказывается полезной. Акустическое давление, как разность мгновенного и постоянного давлений, вызывает движение частиц среды. Разность потенциалов является причиной движения электрических зарядов и в этом смысле акустическое давление аналогично разности потенциалов. Колебательная скорость частиц аналогична скорости движения зарядов и колебательную скорость можно поставить в соответствие току. Тогда аналогично сопротивлению вводится акустическое волновое сопротивление:

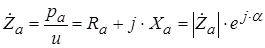(1.22)

где 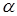- сдвиг по фазе между давлением 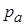и скоростью частиц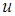

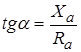
В бегущей плоской волне колебательная скорость (1.20) и давление (1.21) синфазны и акустическое сопротивление равно .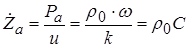

Для воздуха (нормальное атмосферное давление и ):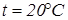

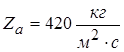
Плоские волны создает, например, круглая пластинка радиусом 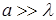, которая совершает колебания, перпендикулярные своей плоскости. На расстояниях 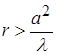фронт уже не будет плоским, волна начнет расходиться. Другой пример плоских, но уже нерасходящихся волн это распространение звука в жесткой трубе с поперечным сечением меньшим .

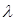Пусть звуковая волна излучается точечным источником, его размеры меньше длины волны. Волна распространяется в однородной среде равномерно по всем направлениям, т.е. потенциал 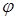зависит только от расстояния 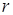от источника и не зависит от угловых координат 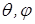. В этом случае мы имеем дело со сферической волной, для которой волновое уравнение принимает вид:

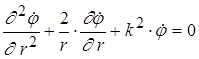
Объединяем два первых слагаемых и получаем уравнение

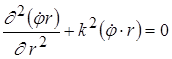, (1.23)

совпадающее с одномерным волновым уравнением (1.19). Решение уравнения (1.23) представляет две сферические волны - расходящаяся волна (бегущая по радиусу 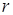) и сходящаяся (бегущая против 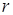). Для сферической волны бегущей по радиусу имеем

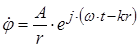(1.24)

где 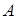- постоянная, зависящая от условий задачи.

В отличии от плоской волны амплитуда сферической волны убывает с расстоянием по закону 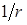. Найдем акустическое давление

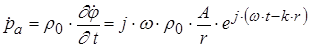(1.25)

Колебательную скорость вычислим по известной формуле

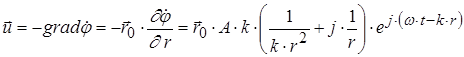
Выделив действительную часть и сделав в ней замену

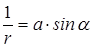
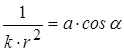
получим

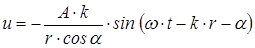(1.26)

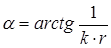(1.27)

Сравнивая давление и скорость (1.25) и (1.26) видим, что для сферической волны колебательная скорость отстает по фазе от давления на величину 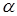, определяемую формулой (1.27). Разность фаз 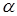быстро уменьшается с расстоянием и с увеличением частоты. Модуль акустического сопротивления равен

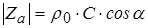
и не превышает сопротивления плоской волны. В дальней зоне 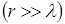сдвиг фаз 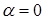, 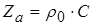и связь между скоростью 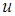и акустическим давлением 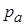такая же, как и для плоской волны.

У цилиндрической осесимметричной волны амплитуда обратно пропорциональна квадратному корню из расстояния от источника, акустическое сопротивление равно

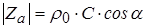, и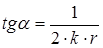

Сдвиг фаз между акустическим давлением и колебательной скоростью появляется только у расходящихся (сходящихся) сферических и цилиндрических волн. Условно это можно пояснить следующим образом. У расходящейся волны слои среды, заключенные между соседними фронтами (например на расстоянии 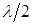) имеют разные массы. Первый слой сталкивается со вторым большей массы, отдает ему энергию и двигается назад, т.е. часть энергии отражается и появляется реактивная составляющая у энергии и у акустического сопротивления. Чем дальше от источника массы слоев выравниваются, уменьшается и реактивная составляющая сопротивления. С уменьшением длины волны массы слоев на расстоянии 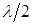отличаются незначительно, уменьшается отражение и соответственно уменьшается сдвиг фаз между колебательной скоростью и звуковым давлением.

Дата добавления: 2015-09-05