Підставимо значення (4.2) та (4.3) в формулу (4.1), отримаємо

F_емп=1,58

За умовою задачі, конкуруюча гіпотеза має вигляд H ₁: D (X) ≠ D (Y), тому критична область – двостороння.

По таблиці Фішера-Снедекора, по рівню значущості, що в двічі менший за заданий, тобто при α/2 = 0,1/2 = 0,05, та кількістю степенів свободи k₁ =50-1=49,k₂ =50-1=49 знаходимо критичну точку F _кр(α/1; k₁, k₂) = (0,05; 49, 49) = 1,6.

Так як критичний критерій менший за емпіричний F _емп > F _кр
(1,66 < 2,5978), то немає підстави відхилити запропоновану гіпотезу, тобто нульова гіпотеза приймається.

Висновок: Результати показують, що вибіркові виправлені дисперсії двох вибірок відрізняються суттєво. Враховуючи, що вибіркові виправлені дисперсії є незміщеними оцінками генеральних дисперсій, то це ж стосується і генеральних дисперсій.

5. Побудова нормальних кривих за дослідними даними.

Для побудови нормальної кривої необхідно визначити емпіричні і теоретичні

(вирівнюючі) частоти.

Емпіричними частотами називають частоти n_i, які фактично спостерігаються Вирівнюючими (теоретичними) називають частоти n_i, які знаходяться

теоретично (обчисленням):

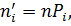(5.1)

де n – кількість спостережень;

P_i – ймовірність значення 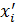ознаки, що спостерігається, за умови, що Х иає невизначений розподіл.

Внашому випадку величина X (генеральна сукупність) розподілена нормально, тому вирівнюючі частоти знаходять за формулою:

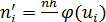, (5.2)

де n - кількість випробувань (обсяг вибірки);

h - довжина часткового інтервалу;

, - вибіркове середнє квадратичне відхилення;

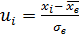; (5.3)

х_в. - вибіркове середнє,

х_і - середина і -го часткового інтервалу;

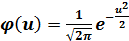(5.4)

Значення функції 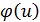наведені в додатку 4.

Нормальну криву за вибірковими даними будуємо наступним чином:

1) Находимо 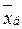і 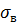із застосуванням будь-якого методу:

Вибіркові дисперсії вибірок Х та Y вже знайдені методом добутків раніше. За формулою 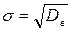знайдемо середні квадратичні відхилення вибірок.

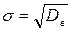(5.5)

Отримаємо:

σ_Xв = 0,96, σ_Yв = 0,77.

Використаємо обраховані раніше умовні моменти першого порядку (див. (2.2)). Знаючи їх можна легко обчислити вибіркові середні за формулою:

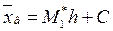
Отримаємо: 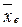= 0,012 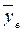= 0,031.

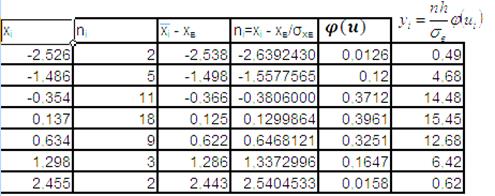
Обчислюємо вирівнюючі частоти для вибіркок Х та У за формулою 5.2, і заносимо у табл.№9(для вибірки Х) та у табл.№10(для вибірки У)

Таблиця №9

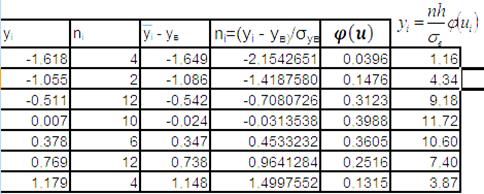
Таблиця №10

Полігон частот будуємо по емпіричним частотам: на координатній площині ставимо точки з координатами (x_i, n_i) (таблиця №5). Точки з’єднуємо прямими лініями.

Нормальну (теоретичну) криву будуємо по вирівнюючим частотам: на координатній площині будуємо точки з координатами (x_i, n_i).

Аналогічні дії проводимо для вибірки Y, тільки значення беремо вже з таблиці №7.

На рис. №3 зображені полігон частот і нормальна крива за вибіркою Х.

На рис. №4 зображені полігон частот і нормальна крива за вибіркою У.

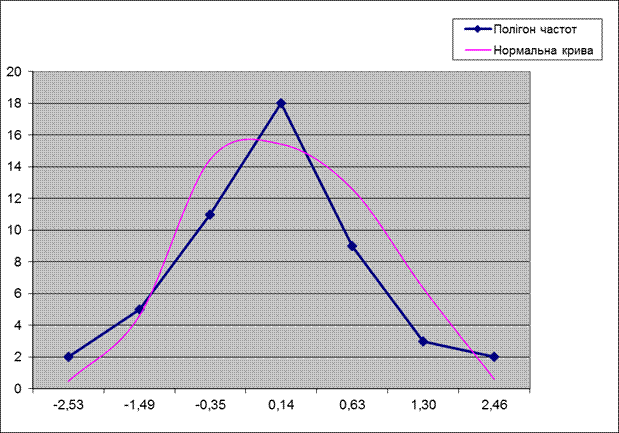
Рис.3 Нормальна крива і полігон частот

Дата добавления: 2015-08-21