Інтервальні оцінки

Необхідно оцінити невідомі математичні сподівання M[X] i M[Y] генеральних сукупностей Х, У за допомогою довірчого інтервалу з надійністю 0,95.

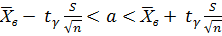(3.1)

де 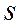- «виправлене» вибіркове середнє квадратичне відхилення, 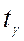знаходять по таблиці додатка 2 за заданими 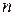і .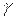

Отже 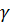= 0,95, n=50.користуючись таблицею значень 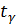(додаток 2), знаходимо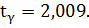

Ми маємо нормально розподілену кількісну ознаку генеральної сукупності. За вибіркою n=50 знайдені вибіркове середнє (з пункту 2):

для вибірки Х: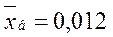

для вибірки Y: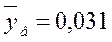

і “виправлене ” середнє квадратичне відхилення:

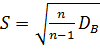(3.2)

D_в ми теж візьмемо з попереднього завдання:

для вибірки Х: 0.925

для вибірки У: 0.586.

і ці значення підсталяємо в формулу(3.2). Отримуємо S:

для вибірки Х: 0,97

для вибірки Y: 0,77

Знайдемо довірчі інтервали для вибірoк Х та Y:

Підставляємо всі значення в формулу (3.1) і отримуємо:

для вибірки Х: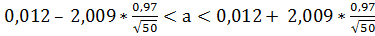

-0,26˂a˂0,29

для вибірки Y: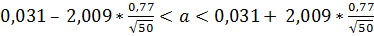

-0,19˂a˂0,25

Висновок: Ми оцінили невідомі математичні сподівання М[Х] і M[У] генеральних сукупностей Х і У за допомогою довірчого інтервалу з надійністю 0,95. Для вибірки Х з надійністю 0,95 невідомий параметр a знаходиться в довірчому інтервалі -0,26 < a < 0,29. Для вибірки Y з надійністю -0,95 невідомий параметр a знаходиться в довірчому інтервалі
-0,19 < a < 0.25.

Дата добавления: 2015-08-21