Враховуючи похибки і округлення, то обчислення виконані правильно.

Тепер знайдемо χ²_кр по таблиці розподілу критичних точок χ² по рівню значущості α = 0,05 і числу степенів свободи k = 7-3 = 4,

χ²_кр = 9,5, .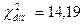

Як бачимо χ²_емп > χ²_кр, отже у нас є підстави відхилити нульову гіпотезу, тобто розходження емпіричних і теоретичних частот відчутне.

Висновок: В результаті перевірки гіпотези про нормальний розподіл генеральних сукупностей X та Y за допомогою критерію погодженості Пірсона можна зробити висновок, що дані спостережень обох вибірок узгоджуються з гіпотезою про нормальний розподіл генеральних сукупностей.

7.. Перевірити гіпотезу про рівність нулю математичних сподівань генеральних сукупностей

За умовою завдання на розрахунково-графічну роботу при якісній роботі досліджуваних систем відхилення вихідного параметра від заданого значення повинне дорівнювати нулю. Тому логічно припустити, що якщо система після дії випадкових факторів повертається у нормальний стан керування, то середнє значення відхилення повинне дорівнювати нулю, інакше матиме місце систематична похибка керування, яка не залежить від дії випадкових факторів, а визначається властивостями системи.

Таким чином, якщо генеральна сукупність розподілена нормально, причому генеральне середнє а невідоме, але є підстави вважати, що воно дорівнює нулю, тобто а = 0,необхідно перевірити гіпотезу пpo рівність нулю генерального середнього. Якщо ця гіпотеза буде прийнята, то будуть підстави для висновку, що система працює без систематичних похибок керування.

Оскільки дисперсія генеральної сукупності невідома, то в якості критерію перевірки нульової гіпотези 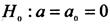приймемо випадкову величину:

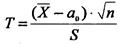(7.1)

де S - „виправлене" середнє квадратичне відхилення;

n - обсяг вибірки;

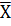- середнє вибіркове.

Величина Т має розподіл Стьюдента з k = n -1 ступенями вільності.

Правило перевірки нульової гіпотези формулюється так.

Правило. Для того, щоб при заданому рівні значущості а перевірити нульову гіпотезу 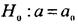про рівність невідомої генеральної середньої а (нормальної сукупності з невідомою дисперсією) гіпотетичному значенню

а = 0 при конкуруючій гіпотезі 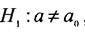, потрібно обчислити спостережене значення критерію 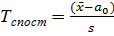і за таблицею критичних точок розподілу Стьюдента (додаток 7), за заданим рівнем значущості а (розміщеним у верхньому рядку таблиці розподілу Стьюдента) і числом ступенів вільності k = n -1 знайти двосторонню критичну точку t_{двост.кр.}(α,k).

Якщо |T_спост| ˂ t_{двост.кр.} - немає підстав відхилити нульову гіпотезу.

Якщо |T_спост| > t_{двост.кр.} - - нульову гіпотезу відхиляють.

Ми маємо нормально розподілену кількісну ознаку генеральної сукупності. За вибіркою n=50 знайдені в попередньому розділі вибіркове середнє:

для вибірки Х: 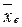= 0,012

для вибірки Y: 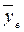= 0,031.

і “виправлене” середнє квадратичне відхилення:

для вибірки Х: 0,97

для вибірки Y: 0,77.

Перевіримо гіпотезу про рівність нулю математичних сподівань генеральних сукупностей Х і У при рівні значущості α= 0,05.

Обчислимо спостережене значення критерію за формулою (7.1) для вибірки Х:

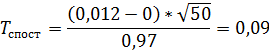
Обчислимо спостережене значення критерію за формулою (7.1) для вибірки Y:

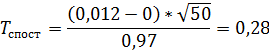
За умовою, конкуруюча гіпотеза має вигляд 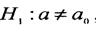, тому критична область двостороння.

За таблицею критичних точок розподілу Стьюдента (додаток 7) за заданим рівнем значущості а= 0,1, розміщеному у верхньому рядку таблиці, і за числом ступенів вільності k=50-1=49 знаходимо критичну точку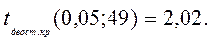

Оскільки |T_спост| ˂ t_{двост.кр.} - немає підстав відхилити гіпотезупро рівність нулю математичних сподівань генеральних сукупностей Х і У.

Висновок: Ми перевірили гіпотезу про рівність нулю математичних сподівань генеральних сукупностей Х і У при рівні значущості α= 0,1.

Обчисливши спостережене значення критерію для обох вибірок, ми дійшли висновку, що немає підстав відхилити гіпотезупро рівність нулю математичних сподівань генеральних сукупностей Х і У, оскільки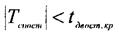

8. Оцінка відхилення емпіричного розподілу від нормального.

Для оцінки відхилення емпіричного розподілу від нормального використовують різні характеристики. Зокрема, до них відносяться асиметрія і ексцес.

Асиметрія емпіричного розподілу визначається за формулою[1, cт.186]:

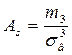, (8.1)

де m ₃ – центральний емпіричний момент третього порядку,

σ_в – вибіркове середнє квадратичне відхилення.

Дата добавления: 2015-08-21