Вибірка Х.

Скористаємось вже обрахованими раніше значеннями умовних варіант.

Отже нехай для вибірки Х: h = 0,75, с = -0,095. Тоді:

від	до	уі	ui	ni	niui	niui^2	niui^3	niui^4	ni(ui+1)^4
-2,526	-1,776	-2,15100	-3		-6		-54
-1,776	-1,03	-1,40300	-2		-10		-40
-1,03	-0,28	-0,65500	-1		-11		-11
-0,28	0,47	0,09500
0,47	1,22	0,84500
1,22	1,97	1,59500
1,97	2,72	2,34500
					-6		-18

Контрольна сума: Σ n_iu_i ⁴ + 4Σ n_iu_i ³ + 6Σ n_iu_i ² + 4Σ n_iu_i + n = 954

де n_i – сума частот і -го інтервалу, u_i – умовні варіанти

Умовні моменти першого та другого порядків другої вибірки були знайдені раніше: , .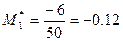

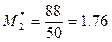Обрахуємо умовні моменти третього та четвертого порядків за формулою (8.5):

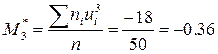
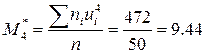
Знайдемо центральні емпіричні моменти третього та четвертого порядків за формулами (8.3) і (8.4):

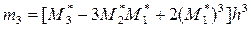=0,114

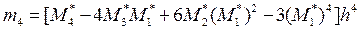=2,98

Знайдемо асиметрію і ексцес за формулами (8.1) і (8.2), вибіркові середні квадратичні знайдені раніше 0,96

. Обраховуємо для вибірки X:

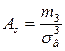= 0,13

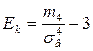= 0,48

Аналогічно працюємо і з вибіркою Y. Скористаємось вже обрахованими раніше значеннями умовних варіант та з таблиці №8. Отже для вибірки Y: h= 0,45
с = -0,268

Від	до	уі	vi	сума частот n	nivi	nivi^2	nivi^3	nivi^4	ni(vi+1)^4
-1,618	-1,168	-1,39300	-3		-12		-108
-1,168	-0,718	-0,94300	-2		-4		-16
-0,718	-0,268	-0,49300	-1		-12		-12
-0,268	0,182	-0,04300
0,182	0,632	0,40700
0,632	1,082	0,85700
1,082	1,532	1,30700

Контрольна сума: Σ n_iu_i ⁴ + 4Σ n_iu_i ³ + 6Σ n_iu_i ² + 4Σ n_iu_i + n = 2168

Умовні моменти першого та другого порядків другої вибірки були найдені раніше: , .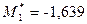

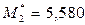Обрахуємо умовні моменти третього та четвертого порядків за формулою (8.5):

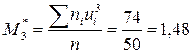
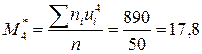
Знайдемо центральні емпіричні моменти третього та четвертого порядків за формулами (8.3) і (8.4):

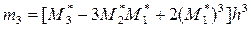= -0,085

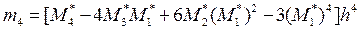= 0,718

Знайдемо асиметрію і ексцес за формулами (8.1) і (8.2), вибіркові середні квадратичні знайдені раніше 0,96

. Обраховуємо для вибірки X:

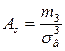= -0,19

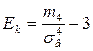= -0,91

Висновок: В даному розділі ми обрахували асиметрію і ексцес для вибірок X та Y.

Асиметрія оцінює видовженість однієї із віток кривої теоретичного розподілу відносно математичного сподівання. Ексцес оцінює „крутизну” кривої теоретичного розподілу відносно нормальної.

9. Представимо математичну модель вибірок за допомогою MatCad2001

Загальна формула:

;

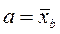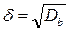
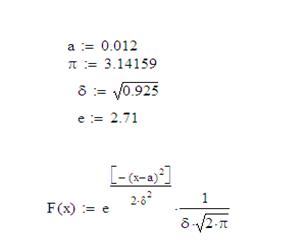Для вибірки Х:

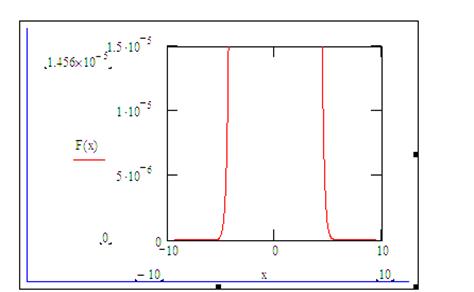Рис.5

Для вибірки У:

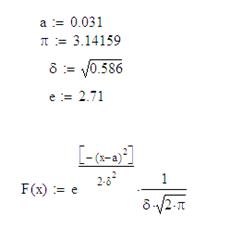
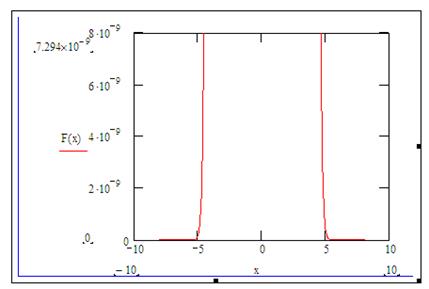Рис.6

10. Висновки:

Після виконання всих поставлених завдань, можна зробити наступні висновки:

Матиматичне сподівання відхилення вибірок становить

для вибірки Х: 0,012

для вибірки Y: 0,031

Середнє квадратичне відхилення

вибірки Х: 0,96

вибірки Y: 0,77

Дисперсія вибірки Х: D_в (X) = 0,925

; вибірки Y: 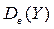= 0,586.

Дані спостережень обох вибірок узгоджуються з гіпотезою про нормальний розподіл генеральних сукупностей.

Генеральні дисперсії двох вибірок відрізняються не значно.

Порівнюючи графіки нормальної кривої і полігону частот можна зробити висновок, що побудована теоретична крива за даними вибірки X (рис. №3) і теоретична крива за даними вибірки Y (рис.№4) відображають дані спостережень досить точно.

Для вибірки Х з надійністю 0,95 невідомий параметр a знаходиться в довірчому інтервалі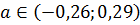

Для вибірки Y з надійністю 0,95 невідомий параметр a знаходиться в довірчому інтервалі .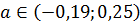

Обчисливши спостережене значення критерію для обох вибірок, ми дійшли висновку, що немає підстав відхилити гіпотезупро рівність нулю математичних сподівань генеральних сукупностей Х і У.

Дата добавления: 2015-08-21