Режим бегущей волны

Режим бегущей волны характеризуется наличием только падающей волны, распространяющейся от генератора к нагрузке. Отраженная волна отсутствует. Мощность, переносимая падающей волной, полностью выделяется в нагрузке. В этом режиме B _U = 0, | Г | = 0, k _св = k _бв = 1

Режим стоячей волны

Режим стоячей волны характеризуется тем, что амплитуда отраженной волны равна амплитуде падающей B _U = A _U то есть энергия падающей волны полностью отражается от нагрузки и возвращается обратно в генератор. В этом режиме, | Г | = 1, k _св = , k _бв = 0

Режим смешанных волн

В режиме смешанных волн амплитуда отраженной волны удовлетворяет условию 0 < B _U < A _U то есть часть мощности падающей волны теряется в нагрузке, а остальная часть в виде отраженной волны возвращается обратно в генератор. При этом 0 < | Г | < 1, 1 < k _св < , 0 < k _бв < 1

Модели нелинейных элементов. Модели безинерционных нелинейных элементов. Аппроксимация характеристик нелинейных элементов. Постановка задачи аппроксимации. Кусочно-линейная аппроксимация. Полиномиальная аппроксимация. Метод выбранных точек. Метод наименьших квадратов.

Нелинейные элементы – это такие элементы системы автоматического управления, выходная переменная которых не зависит от скорости изменения входной величины.

Линейный безынерционный элемент полностью задается значением его коэффициента усиления. Нелинейные зависимости между постоянными значениями входных и выходных сигналов

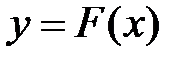
могут задаваться аналитически, графически или таблично. В том случае, когда нелинейный элемент (НЭ) имеет один вход и один выход особенно наглядны графики статических характеристик (СХ) (рис. 9.5).

Условия преобразования сигналов безынерционными НЭ зависят от уровней сигналов и не зависят от их частоты.

1. Нелинейные элементы с кусочно-постоянными СХ. Простейшим представителем нелинейностей этой группы является так называемое идеальное реле (рис. 9.6, а):

(9.5)

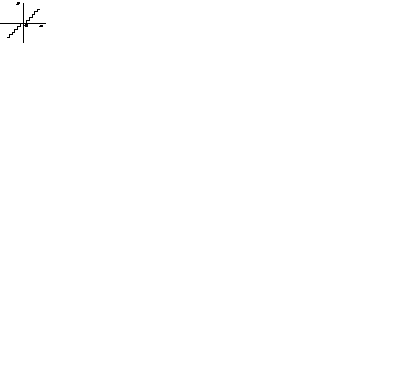
а б в

Рис. 9.6. Кусочно-постоянные (релейные) СХ

2. Нелинейные элементы с кусочно-линейными СХ. На рис. 9.7, а показан график СХ НЭ типа “насыщение”:

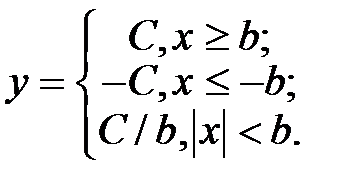
Как правило, эта нелинейность вводится в модели для учета ограничений уровней переменных при исследовании поведения систем управления в режимах больших отклонений от положения равновесия.

а б в

Нелинейные элементы с гладкими СХ. Гладкие СХ имеют непрерывные производные. Примерами являются характеристики термопары (рис. 9.8, а), устройства возведения входного сигнала в квадрат (рис. 9.8, б), в куб (рис. 9.8, в), индукционных электромеханических преобразователей угла, электромагнитных явлений с гистерезисом (см. рис. 9.5) и др.

Нелинейные зависимости между значениями входа и выхода можно задавать параметрически ― парой функций

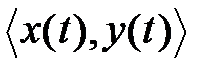.Аппроксимация степенным полиномом

Для транзистора: I – ток коллектора, U - напряжение на базе; для лампы: I – анодный ток, U – напряжение на сетке.

; ; .

При заданной форме вольт-амперной характеристики коэффициенты определяются положением рабочей точки на характеристике

Дата добавления: 2015-08-21