Метод узловых потенциалов. Определение числа независимых уравнений. Матричная запись системы уравнений. Полная матрица узлов (матрица инциденций). Примеры.

Метод узловых напряжений (потенциалов) заключается в том, что на основании первого закона Кирхгофа определяются напряжения в узлах электрической цепи относительно некоторого базисного узла. Эти искомые напряжения называются узловыми напряжениями. Зная узловые напряжения в электрической цепи можно найти токи в ветвях.

Запишем 1-й закон Кирхгофа для всех независимых узлов: 1/(jωc₁)+1/(jωc₂)=1/(jωc_э), где с_э - эквивалентная емкость. с_э=(с₁*с₂)/(с₁+с₂)

q – узлов, p – ветвей, N_н – идеальных источников напряжений.

Число независимых уравнений: N_y=q-1-N_H. Либо с помощью Графа и его дерева, по количеству ветвей графа определяем количество не зависимых уравнений.

Полная матрица узлов (используются также другие названия этой матрицы: полная матрица инциденций, матрица соединений, структурная матрица) – это таблица, в которой число столбцов равно числу ветвей графа , а число строк равно числу узлов . Номера строк совпадают с номерами узлов (строка с нулевым номером обычно располагается последней), номера столбцов совпадают с номерами ветвей. 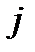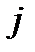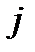Элемент матрицы , расположенный на пересечении -й строки и -го столбца, может принимать значения +1, -1 и 0: , если ветвь инцидентна узлу и направлена от этого узла; , если ветвь инцидентна узлу и направлена к этому узлу; , если ветвь 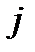не инцидентна узлу .

В соответствии с первым законом Кирхгофа окончательно имеем

Матричная запись системы уравнений.

, , , это вид матриц. Уравнение имеет вид

18. Метод суперпозиции. Ограничения на применимость метода.

Дата добавления: 2015-08-21