Выбор положительных направлений для токов и напряжений.

Законы Кирхгофа для мгновенных значений токов и напряжений

Выбор положительных направлений для токов и напряжений.

Первый закон Кирхгофа устанавливает связь между токами ветвей в каждом из узлов цепи: алгебраическая сумма мгновенных значений токов всех ветвей, подключенных к каждому из узлов моделирующей цепи, в любой момент времени равна нулю.

В соответствии с первым законом Кирхгофа для каждого из узлов может быть составлено уравнение баланса токов в узле: ∑ i_k=0 где номер ветви, подключенной к рассматриваемому узлу.

Суммирование токов производится с учетом выбранных положительных направлений: всем токам, одинаково ориентированным относительно узла, приписывается одинаковый знак.

Второй закон Кирхгофа устанавливает связь между напряжениями ветвей, входящих в произвольный контур: алгебраическая сумма мгновенных значений напряжений всех ветвей, входящих в любой контур моделирующей цепи, в каждый момент времени равна нулю.

В соответствии со вторым законом Кирхгофа для каждого контура можно составить уравнения баланса напряжении ветвей: ∑u_k=0 где - номера ветвей, входящих в рассматриваемый контур.

Суммирование напряжений производится с учетом их положительных направлений и выбранного направления обхода контура. Если положительное направление напряжения ветви совпадает с направлением обхода контура, то оно входит в формулу со знаком плюс, в противном случае – со знаком минус.

Уравнения по второму закону Кирхгофа можно составить не только для напряжений ветвей, но и для напряжений элементов, входящих в ветви каждого контура, представляя напряжение каждой ветви в виде суммы напряжений элементов этой ветви и принимая во внимание, что положительное направление напряжения источника э. д. с. противоположно направлению
э. д. с.:

Тогда второй закон будет выглядеть: алгебраическая сумма мгновенных значений напряжений на элементах любого контура моделирующей цепи в каждый момент времени равна алгебраической сумме мгновенных значений э. д. с. источников напряжения, действующих в этом контуре.

Напряжения на элементах контура и
э. д. с. источников напряжения входят в со знаком плюс, если положительные направления напряжений на элементах и направления э. д. с. источников напряжения совпадают с направлением обхода контура

Эл. цепь синусоидального тока. Амплитуда, частота, нач. фаза гармонич. тока (напряжения). Разность фаз. Ср. знач. за период гармонич. функции, ср. полупериодное значение, действующее или эффективное или среднеквадратич. значение гармонич. функции.

Эл. цепь – совокупность устройств и объектов, образующих путь для эл. тока, электромагнитные процессы в которой можно описать понятиями ЭДС, тока и напряжения.

Синусоидальный ток – ток, амплитуда которого изменяется по гармонич. закону синусоиды.

Амплитуда – макс. значение гармонич. изменяющейся величины.

Частота – число периодов в ед. времени.

Нач. фаза – смещение гармонич. сигнала относительно начала координат (t=0).

Разность фаз – величина, равная разности нач. фаз 2-х гармонич. сигналов.

Ср. знач. за период – у гармонич. функции равно нулю.

Ср. полупериодное значение - 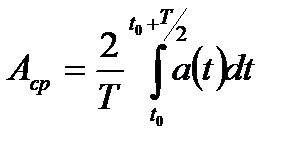, где a(t) – гармонич. функция, Т – период.

Действ. значение – для гармонич. функции оно в √2 раз меньше её амплитуды.

Дата добавления: 2015-08-21