
Читайте также:
|
Реакция линейных цепей на произвольное внешнее воздействие, представляющее собой линейную комбинацию более простых воздействий, равна линейной комбинации реакций, вызванных каждым из простых воздействий в отдельности.
Из теоремы наложения следует, что ток или напряжение любой ветви линейной электрической цепи, содержащей наряду с пассивными элементами зависимые и независимые источники тока и напряжения, равны сумме частичных токов или напряжений, вызванных действием каждого независимого источника в отдельности.
На теореме наложения основан широко используемый на практике метод анализа цепей — метод наложения. Его удобно применять в тех случаях, когда по условиям задачи требуется определить ток или напряжение одной из ветвей электрической цепи, в состав которой входит несколько независимых источников. В соответствии с теоремой наложения искомый ток (напряжение) представляют в виде суммы частичных токов (напряжений). Для определения частичных токов (напряжений) используют эквивалентные схемы цепи, получаемые из исходной путем выключения всех независимых источников, кроме одного, вызывающего соответствующий частичный ток (напряжение). Таким образом, задача анализа сложной цепи, содержащей несколько независимых источников энергии, заменяется рядом более простых задач по исследованию цепей с одним независимым источником.
Метод наложения применим только для определения токов или напряжений линейной электрической цепи и не может быть использован для нахождения величин, которые не являются линейными функциями токов или напряжений.
19. Мощность в цепи синусоидального тока в комплексной форме. Условие передачи максимума активной мощности от источника в нагрузку.
Комплексное число  , модуль которого равен полной мощности цепи
, модуль которого равен полной мощности цепи 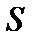 , а аргумент - углу сдвига фаз между током и напряжением
, а аргумент - углу сдвига фаз между током и напряжением  , называется комплексной мощностью цепи
, называется комплексной мощностью цепи  . (2.71) Переходя от показательной формы записи
. (2.71) Переходя от показательной формы записи  к тригонометрической
к тригонометрической  , (2.72) устанавливаем, что вещественная часть комплексной мощности равна активной мощности цепи:
, (2.72) устанавливаем, что вещественная часть комплексной мощности равна активной мощности цепи:  . (2.73) Мнимая часть комплексной мощности представляет собой так называемую реактивную мощность цепи
. (2.73) Мнимая часть комплексной мощности представляет собой так называемую реактивную мощность цепи  . (2.74) Реактивная мощность характеризует процессы обмена энергией между цепью и источником и численно равна максимальной скорости запасания энергии в цепи. С учетом (2.73) и (2.74) выражение (2.72) можно записать следующим образом:
. (2.74) Реактивная мощность характеризует процессы обмена энергией между цепью и источником и численно равна максимальной скорости запасания энергии в цепи. С учетом (2.73) и (2.74) выражение (2.72) можно записать следующим образом: 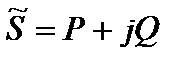 . (2.75) Отсюда следует, что комплексная мощность представляет собой комплексное число, вещественная часть которого равна активной мощности цепи
. (2.75) Отсюда следует, что комплексная мощность представляет собой комплексное число, вещественная часть которого равна активной мощности цепи  , а мнимая - реактивной
, а мнимая - реактивной  . Комплексному числу
. Комплексному числу  можно поставить в соответствие вектор
можно поставить в соответствие вектор  , проекции которого на вещественную и мнимую оси равны, соответственно
, проекции которого на вещественную и мнимую оси равны, соответственно 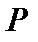 и
и  (рис. 2.16, а). Прямоугольный треугольник с гипотенузой, равной
(рис. 2.16, а). Прямоугольный треугольник с гипотенузой, равной  , и катетами
, и катетами  и
и  называется треугольником мощностей. Из рисунка видно, что полная, активная и реактивная мощности связаны между собой соотношением
называется треугольником мощностей. Из рисунка видно, что полная, активная и реактивная мощности связаны между собой соотношением  . В связи с тем что треугольник мощностей цепи подобен треугольнику сопротивлений этой же цепи (рис. 2.16, б), комплексная мощность
. В связи с тем что треугольник мощностей цепи подобен треугольнику сопротивлений этой же цепи (рис. 2.16, б), комплексная мощность  и её компоненты
и её компоненты  ,
,  ,
,  могут быть выражены через комплексное сопротивление цепи
могут быть выражены через комплексное сопротивление цепи  и его компоненты
и его компоненты  ,
,  ,
,  :
:  ;
; 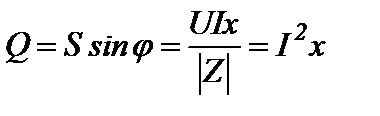 ;
;  ;
;  . (2.76) Найдем связь между комплексной мощностью и комплексными действующими значениями тока и напряжения на зажимах цепи. Подставляя в (2.71) выражения (2.69) и (2.20), находим
. (2.76) Найдем связь между комплексной мощностью и комплексными действующими значениями тока и напряжения на зажимах цепи. Подставляя в (2.71) выражения (2.69) и (2.20), находим
 , (2.77)
, (2.77)
где 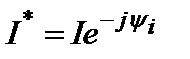 - число, комплексно сопряженное с
- число, комплексно сопряженное с  (комплексно сопряженный ток).
(комплексно сопряженный ток).
Таким образом, комплексная мощность цепи равна произведению комплексного напряжения цепи 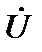 на комплексно сопряженный ток
на комплексно сопряженный ток  .
.
Полная мощность численно равна амплитуде переменной составляющей мгновенной мощности. Активная мощность двухполюсника может быть выражена через полную мощность:
 . (2.70)
. (2.70)
Из выражения (2.70) видно, что полная мощность есть максимально возможное, значение активной мощности цепи, которое имеет место при  .
.
20. Баланс мощностей в цепи синусоидального тока в комплексной форме.
Рассмотрим произвольную электрическую цепь, содержащую 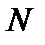 идеальных источников напряжения,
идеальных источников напряжения,  идеальных источников тока и
идеальных источников тока и 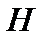 идеализированных пассивных элементов.
идеализированных пассивных элементов.
 . (2.80)
. (2.80)
Уравнение (2.80) называется уравнением (условием) баланса комплексных мощностей. Таким образом, сумма комплексных мощностей, отдаваемых всеми идеализированными активными элементами, равна сумме комплексных мощностей всех идеализированных пассивных элементов.
Для практических расчётов электрических цепей условие баланса мощностей удобно представить в следующей форме
 . (2.81)
. (2.81)
Левая часть выражения (2.81) представляет собой алгебраическую сумму комплексных мощностей, отдаваемых всеми активными элементами. Слагаемое вида  есть произведение комплексного действующего значения
есть произведение комплексного действующего значения
э. д. с. источника напряжения на комплексно сопряженный ток этого источника; слагаемое вида  равно произведению комплексного напряжения на источнике, тока на комплексно сопряженный ток этого источника. Из условия баланса комплексных мощностей следуют условия баланса активных и реактивных мощностей: активная мощность, отдаваемая всеми источниками, равна активной мощности всех потребителей:
равно произведению комплексного напряжения на источнике, тока на комплексно сопряженный ток этого источника. Из условия баланса комплексных мощностей следуют условия баланса активных и реактивных мощностей: активная мощность, отдаваемая всеми источниками, равна активной мощности всех потребителей:
 ;
;
реактивная мощность всех источников равна реактивной мощности всех потребителей:
 ,
,
где  и
и 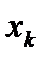 - вещественная и мнимая составляющие комплексного сопротивления
- вещественная и мнимая составляющие комплексного сопротивления  -го элемента.
-го элемента.
Дата добавления: 2015-08-21; просмотров: 267 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Метод узловых потенциалов. Определение числа независимых уравнений. Матричная запись системы уравнений. Полная матрица узлов (матрица инциденций). Примеры. | | | Линейный трансформатор при гармоническом воздействии. |