Последовательная RLC-цепь
Используя законы Ома и Кирхгофа в комплексной форме, составим систему уравнений электрического равновесии цепи
 ;
;  ;
;
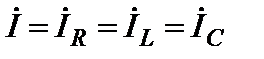 ;
;  ; (2.63)
; (2.63)
 . где
. где  ;
;  ;
;  - комплексные сопротивления входящих в цепь идеализированных элементов. Решая систему (2.63) относительно тока
- комплексные сопротивления входящих в цепь идеализированных элементов. Решая систему (2.63) относительно тока  , получаем
, получаем  . (2.64) Здесь
. (2.64) Здесь  - комплексное входное сопротивление последовательной RLC-цепи, равное сумме комплексных сопротивлений входящих в цепь элементов, которое определяется только параметрами входящих в цепь элементов и частотой внешнего воздействия:
- комплексное входное сопротивление последовательной RLC-цепи, равное сумме комплексных сопротивлений входящих в цепь элементов, которое определяется только параметрами входящих в цепь элементов и частотой внешнего воздействия:  . (2.65)
. (2.65)
| Рис. 2.15. Векторные диаграммы для тока и напряжений последовательной RLC-цепи
|
Переходя от алгебраической формы записи  к показательной, находим модуль и аргумент комплексного входного сопротивления:
к показательной, находим модуль и аргумент комплексного входного сопротивления: 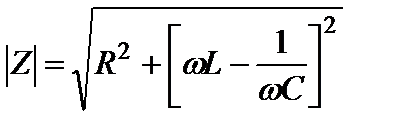 ;
;  ; (2.66)
; (2.66)
Из выражения (2.66) следует, что характер входного сопротивления цепи зависит от соотношения между мнимыми составляющими комплексного входного сопротивления ёмкости  и индуктивности
и индуктивности 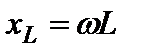 . При
. При  входное сопротивление цепи имеет резистивно-индуктивный характер (
входное сопротивление цепи имеет резистивно-индуктивный характер ( ). Векторная диаграмма, построенная на основании выражения (2.65) и иллюстрирующая данный случай, представлена на
). Векторная диаграмма, построенная на основании выражения (2.65) и иллюстрирующая данный случай, представлена на
рис. 2.14, г (для большей наглядности векторы  и
и 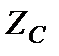 изображены немного смещенными один относительно другого). Если
изображены немного смещенными один относительно другого). Если  , то входное сопротивление цепи имеет резистивно-емкостной характер (
, то входное сопротивление цепи имеет резистивно-емкостной характер ( ) (рис. 2.14, д). При
) (рис. 2.14, д). При  мнимые составляющие входного сопротивления емкости
мнимые составляющие входного сопротивления емкости  и индуктивности
и индуктивности  взаимно компенсируются и входное сопротивление цепи имеет чисто резистивный характер (
взаимно компенсируются и входное сопротивление цепи имеет чисто резистивный характер ( )
)

|
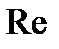
|

|

|
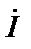
|

|

|

|

|
Используя уравнение (2.64), можно по известному напряжению, приложенному к внешним зажимам цепи, найти ток и наоборот (рис.2.15).
Падение напряжения на сопротивлении  , совпадает по направлению с током
, совпадает по направлению с током 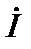 ; напряжение
; напряжение  сдвинуто по фазе относительно
сдвинуто по фазе относительно  на
на  (опережает ток); напряжение
(опережает ток); напряжение  отстает по фазе от тока на
отстает по фазе от тока на  и направлено в противоположную сторону
и направлено в противоположную сторону  . При
. При  сумма
сумма  совпадает по направлению с вектором
совпадает по направлению с вектором  , ток цепи отстает по фазе от напряжения (
, ток цепи отстает по фазе от напряжения ( ) При
) При 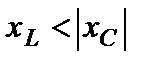 сумма
сумма 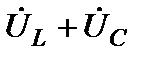 совпадает по направлению с вектором
совпадает по направлению с вектором  , ток цепи опережает по фазе напряжение (
, ток цепи опережает по фазе напряжение ( ) Если
) Если  , то сумма
, то сумма  , напряжение на зажимах цепи
, напряжение на зажимах цепи  равно напряжению на сопротивлении
равно напряжению на сопротивлении 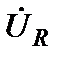 , ток цепи совпадает по фазе с приложенным напряжением (
, ток цепи совпадает по фазе с приложенным напряжением ( ).
).
Дата добавления: 2015-08-21; просмотров: 414 | Нарушение авторских прав
Читайте в этой же книге: Выбор положительных направлений для токов и напряжений. | Энергия, мгновенная мощность, средняя мощность электрических колебаний. | Метод комплексных амплитуд. Ограничения на его применение. | КЧХ последовательного колебательного контура, входное сопотивление, входная проводимость. | Сопротивление параллельного контура с параллельным включением | Комплексные частотные характеристики последовательного колебательного контура | Определение числа независимых контуров. Матричная запись системы уравнений. Матрица главных контуров. Примеры. | Метод узловых потенциалов. Определение числа независимых уравнений. Матричная запись системы уравнений. Полная матрица узлов (матрица инциденций). Примеры. | Теорема наложения (суперпозиции) | Линейный трансформатор при гармоническом воздействии. |
mybiblioteka.su - 2015-2026 год. (0.065 сек.)

 ;
;  ;
;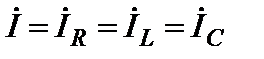 ;
;  ; (2.63)
; (2.63) . где
. где  ;
;  ;
;  - комплексные сопротивления входящих в цепь идеализированных элементов. Решая систему (2.63) относительно тока
- комплексные сопротивления входящих в цепь идеализированных элементов. Решая систему (2.63) относительно тока  , получаем
, получаем  . (2.64) Здесь
. (2.64) Здесь  - комплексное входное сопротивление последовательной RLC-цепи, равное сумме комплексных сопротивлений входящих в цепь элементов, которое определяется только параметрами входящих в цепь элементов и частотой внешнего воздействия:
- комплексное входное сопротивление последовательной RLC-цепи, равное сумме комплексных сопротивлений входящих в цепь элементов, которое определяется только параметрами входящих в цепь элементов и частотой внешнего воздействия:  . (2.65)
. (2.65)








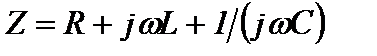





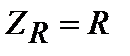











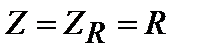






 к показательной, находим модуль и аргумент комплексного входного сопротивления:
к показательной, находим модуль и аргумент комплексного входного сопротивления: 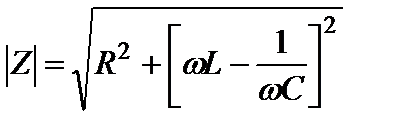 ;
;  ; (2.66)
; (2.66)
 и индуктивности
и индуктивности 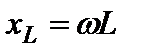 . При
. При  входное сопротивление цепи имеет резистивно-индуктивный характер (
входное сопротивление цепи имеет резистивно-индуктивный характер ( ). Векторная диаграмма, построенная на основании выражения (2.65) и иллюстрирующая данный случай, представлена на
). Векторная диаграмма, построенная на основании выражения (2.65) и иллюстрирующая данный случай, представлена на  и
и 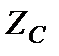 изображены немного смещенными один относительно другого). Если
изображены немного смещенными один относительно другого). Если  , то входное сопротивление цепи имеет резистивно-емкостной характер (
, то входное сопротивление цепи имеет резистивно-емкостной характер ( ) (рис. 2.14, д). При
) (рис. 2.14, д). При  мнимые составляющие входного сопротивления емкости
мнимые составляющие входного сопротивления емкости  и индуктивности
и индуктивности  взаимно компенсируются и входное сопротивление цепи имеет чисто резистивный характер (
взаимно компенсируются и входное сопротивление цепи имеет чисто резистивный характер ( )
)
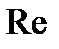


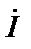




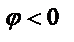

















 , совпадает по направлению с током
, совпадает по направлению с током 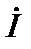 ; напряжение
; напряжение  сдвинуто по фазе относительно
сдвинуто по фазе относительно  на
на  (опережает ток); напряжение
(опережает ток); напряжение  отстает по фазе от тока на
отстает по фазе от тока на  и направлено в противоположную сторону
и направлено в противоположную сторону  . При
. При  сумма
сумма  совпадает по направлению с вектором
совпадает по направлению с вектором  , ток цепи отстает по фазе от напряжения (
, ток цепи отстает по фазе от напряжения ( ) При
) При 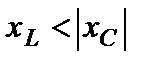 сумма
сумма 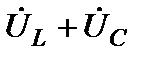 совпадает по направлению с вектором
совпадает по направлению с вектором  , ток цепи опережает по фазе напряжение (
, ток цепи опережает по фазе напряжение ( ) Если
) Если  , то сумма
, то сумма  , напряжение на зажимах цепи
, напряжение на зажимах цепи  равно напряжению на сопротивлении
равно напряжению на сопротивлении 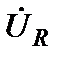 , ток цепи совпадает по фазе с приложенным напряжением (
, ток цепи совпадает по фазе с приложенным напряжением ( ).
).