Комплексные частотные характеристики последовательного колебательного контура

Частотные характеристики контура будем рассматривать в режиме холостого хода(для параллельного аналогично последовательному) (рис.6.9):

-комплексная входная проводимость: ; (6.29)

-комплексный коэффициент передачи по напряжению для случая, когда напряжение снимается с емкости:

; (6.30)

-комплексный коэффициент передачи по напряжению для случая, когда напряжение снимается с индуктивности:

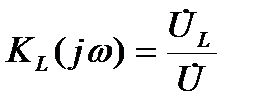(6.31)

Y(x,)   0,7   q(x) p/2   -p/2    

-1 0 1 x,

x,  

Комплексный ток контура определяется произведением комплексной входной проводимости контура на комплексное действующее значение э.д.с.. При постоянных действующем значении входного напряжения и нулевой начальной фазе зависимость нормированного входного тока контура от частоты совпадает с нормированной амплитудно-частотной характеристикой входной проводимости контура, а зависимость начальной фазы от частоты совпадает с нормированной фазо-частотной характеристикой контура.

Рис 6.13. Нормированные АЧХ и ФЧХ комплексной проводимости последовательного колебательного контура.

(6.37)

(6.38)

На резонансной частоте

-входное сопротивление контура имеет чисто резистивный характер и равно сопротивлению потерь контура: Z(₀) = R;

-действующее значение тока контура I = U/R;

где U — действующее значение напряжения на контуре;

-полное сопротивление емкости равно полному сопротивлению индуктивности:

-

(6.16) (6.17)

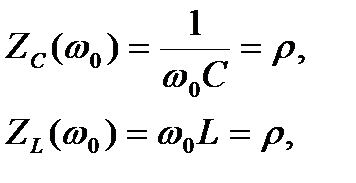
где  - характеристическое сопротивление - сопротивление емкости или индуктивности контура на резонансной частоте. С учётом (6.14)  =₀ L=1 /(₀ С)= 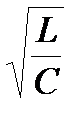; (6.18)

-действующие значения напряжений на реактивных элементах контура U_C(₀) = U_L(₀) = I. (6.19)

Отношение действующего значения напряжения на реактивном элементе контура к действующему значению напряжения на контуре на резонансной частоте называется добротностью контура

(6.20)

Используя выражение (6.18), добротность колебательного контура Q можно выразить через параметры его элементов:

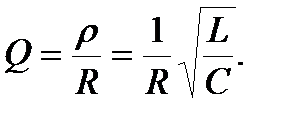
- связь резонансной частоты и добротности

Как правило, добротность колебательных контуров современной радиотехнической аппаратуры лежит в пределах от нескольких десятков до нескольких сотен, поэтому в режиме резонанса напряжение на реактивных элементах контура может во много раз превышать приложенное к контуру напряжение. При неизменной резонансной частоте ₀ добротность контура растет с увеличением характеристического сопротивления контура и с уменьшением сопротивления потерь.

Полоса пропускания реальных избирательных устройств условно определяется как диапазон частот, в пределах которого амплитуда отклика цепи не падает ниже уровня 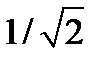= 0,707 от максимального значения. На частотах, соответствующих границам полосы пропускания, амплитуда отклика составляет 0,7от максимального значения, а потребляемая цепью активная мощность в 2 раза меньше максимальной.

(6.48)

Ширина полосы пропускания пропорциональна резонансной частоте контура

2  = _в – _н = ₀/Q. (6.49)

Таким образом, избирательные свойства последовательного колебательного контура зависят от его добротности: чем выше добротность контура, тем меньше ширина полосы пропускания.

Дата добавления: 2015-08-21