Луивилль теоремасы

Барлық комплексті C жазықтығында f голоморфты болсын және M > 0,

барлығы үшін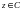

Онда f(z)≡const.

Дәлелдеу. Тейлор f функциясының a=0 нүктесінде C_n коэффициенттері арқылы белгілейміз.

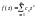
Барлығы үшін 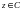. Коши теңсіздігіне сәйкес

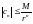
Барлығы үшін r > 0 және n = 0,1,2,.... r → ∞ ұмтылдыра біз n = 1,2,.... кезіндегі 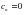аламыз.

Осылайша,f(z) = c₀≡ const.

Ескерту. Луивилль теоремасы бойынша барлық С жазықтығында константалардан басқа шектеулі голоморфты функция жоқ. Әр үзіліссіз функция шартта шектеулі болғандықтан, кеңейтілген комплексті жазықтығында жалғыз голоморфты функция константалар болып табылады.

Голоморфты функциялардың шексіз рет дифференциалдану. Морера теоремасы.

Голоморфты функция. ∞ ∈ аймағында берілген комплекс мәнді f функциясы 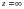нүктесінде голоморфты деп аталады, егер функция

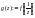
нөлде голоморфты болса.

Анықтама. 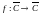шексіздікке 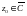нүктесінде ұмтылса, z₀нүктесінде голоморфты деп аталады:

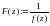
Көбінесе, егер f(∞) = ∞ болса,онда f голоморфтылығы z₀= ∞ нүктесінде функцияның нөлде голоморфтылығын білдіреді

.

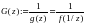Дата добавления: 2015-09-03