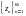Тізбектер

_{комплекс сандар тізбегі деп оң бүтін сандарда анықталған функцияны айтамыз.}

А н ы қ т а м а. саны 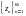комплекс сандар тізбегінің шегі деп аталады, егер кез келген саны үшін номері табылып, барлық үшін теңсіздігі орындалса.

Ақырлы шегі бар тізбек жинақты тізбек деп аталып, түрінде жазылады. Бұл 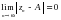жазуымен эквивалентті.

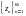комплекс сандар тізбегінің шегі шексіздік деп аталады, егер кез келген Мсаны үшін номері табылып, барлық үшін 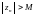теңсіздігі орындалса.

Әрбір комплекс сандар тізбегі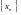не және нақтысандар тізбектері сәйкес келеді.

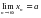1-теорема. шегі бар болуы үшін, және 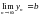шектерінің бар болуы қажетті және жеткілікті.

Жинақты комплекс сандар тізбектері үшін жинақты нақты сандар тізбектері үшінорындалатын қасиеттер орынды. Егер және болса, онда , , ал блса, онда .

2-теорема (Кошикритерийі). тізбегі жинақты болуы үшін ол тізбектің фундаментальді болуы қажетті және жеткілікті, яғни кез келген саны үшін саны табылып, барлық және 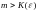нөмірлері үшін теңсіздігі орындалса.

3-теорема (Больцано-Вейерштрасс). Кез келген шенелген тізбектен кемінде бір ақырлы шегі бар болатын тізбекше бөліп алуға болады.

4-теорема. Кеңейтілген комплекс жазықтығында кез келген тізбектен кемінде бір ақырлы, әлде ақырсызшегі бар болатын тізбекше бөліп алуға болады.

Комплекс сандар жиынын¥символымен толықтау. (Риман сферасына) стереографикалық проекция кеңейтiлген комплекс сандар жиынын геометриялық бейнелеу ретінде, оның қасиеттерi. Екі бейнелеулерге сәйкес комплекс сандар жиынындағы екі метрика.Бекітілген дөңгелектің нүктелері үшін олардың эквивалентілігі.

Әрбір , , 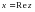, комплекс саннына абсцисасы және ординатасы болатын нүктесі немесе ОМ векторы сәйкес келтіріледі. Векторларды қосу сәйкес комплекс сандарды қосуды білдірелі. Комплекс сандар бейнеленген жазықтық комплекс жазықтық деп, Х– осі нақты ось, ал У – жорамал ось деп аталады.Ақырлы комплекс жазықтық С арқылы белгіленеді. нүктесімен толықтырылған комплекс жазықтық, кеңейтілгенкомплекс жазықтық деп, алол проекцияланатын сфера – Риман сферасы деп аталады.Кеңейтілген комплекс жазықтық символымен белгіленеді.Комплекс жазықтықтың 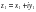және нүктелерінің ара қашықтығы аналитикалық геометриядан белгілі

(1)

формуламен анықталады. Басқаша айтқанда, (1) формула жазықтығында метриканы анықтайды.

Комплекс мүшелі сандық қатарлар. С-дағы қатардың жинақталуы мен екі нақты мүшелі қатарлардың жинақталуымен байланысы. Жинақталудың жеткілікті шарты. Абсолютті, шартты жинақталатын қатарлар. Қатар жинақтылығының жеткілікті шарттары, Коши, Д’аламбер белгілері. Комплекс облыстағы қатарлар теориясы математикалық анализ курсындағы қатарлар теориясы сияқты құрылады.Мүшелері комплекс сандар болатын

, (1)

қатары берісін.

, қатар мүшелері, ал —қатардың жалпы мүшесі деп аталады.

қосындыларын қатардың дербес қосындылары деп атайды.

А н ы қ т а м а. Егер сандық тізбегінің S -қатең шегі бар болса, онда (1) қатары жинақталады, S саны (1) қатарының қосындысы дейді.

Бұл жағдайда «(1) қатары S санына жинақталады» деп те атайды. Қалған жағдайлардың әрқасысында, яғни тізбегінің , не ақырсыз шектері бар не ешқандай да шегі болмағанда, (1) қатары жинақталмайды, не жинақсыз дейді.

16-теорема (Қатар жинақтылығының қажетті шарты).

Егер қатары жинақталса, онда оның, жалпымүшесініңшегібаржәненольгетең,яғни, .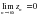

Салдар(қатаржинақталмауыныңжеткіліктішарты). Егерқатардың.жалпымүшесінольгеұмтылмаса, ондақатаржинақталмайды.

Е.скерту. 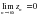шартықатаржинақталуыныңқажеттішартыболатұрып, жеткіліктішартыемес: қатардыңжалпымүшесінольгеүмтылсада, қатаржииақталмауымүмкін.

Теорема17. Мүшелері комплекс сандар болатын қатары жинақталуы үшін, оның нақты және жорамал бөліктері болатын және қатарларының жинақталы қажетті және жеткілікті.

Анықтама. (1) қатар абсолютжинақты деп аталады, егер оның мүшелерінің модульдерінен тұратын қатары жинақты болса.

Салыстыру белгісі. Егер барлық үшін болса онда жинақтылығынан жинақтылығы шығады.

Даламбер белгісі. Егер болып, болса (1) қатар абсолют жинақты, ал болса жинақсыз.

С мағынасында С-да жататын шенелген жиындар. мағынасында -да жататын жиынның шенелуі. С-дағы және - дағы облыстар. Байланыстық және сызықтық байланыстық.

А н ы қ т а м а. Жазықтықтағы нүктелердің D жиыны ашық деп аталады, егер нүктелерінің барлығы D жиынының ішкі нүктелері болса.

Мысалы, сақинасы ашық жиын.

А н ы қ т а м а. Ашық D жиыны облыс деп аталады, егер ол байланысты болса, яғни кез келген нүктелерін толығымен D –да жататын 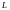сызығымен жалғауға болса.

Мысалы, жиыны облыс.

Екі дөңгелек и нүктелерінен тұратын D жиыны ашық, бірақ байланысты емес. Мысалы, осы шеңберлер ценрі болатын -1 және +1 нүктелерін барлық нүктелері D да жататын, қисығымен қоса алмаймыз.

А н ы қ т а м а. Ашық жиынның барлық шектік нүктелерінің жиынтығы оның шекарасы деп аталады.

Мысалы, сақинасының шекарасы и шеңберлер болады. Тұйық сақина 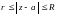теңсіздіктерімен анықталады.

А н ы қ т а м а. Жазықтықтың D нүктелер жиыны шенелген деп аталады, егер болатындай дөңгелегі бар болса.

Мысалы, дөңгелегі шенелген жиын. Себебі, болғанда болады. Жоғарғы жарты жазықтық 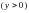шенелмеген жиын.

С жазықтығындағы облыстар бірбайланысты және көпбайланысты болып бөлінеді.

А н ы қ т а м а. облысы бірбайланысты деп аталады, егер осы облыста жатқан кез келген тұйық (үзіліссіз) қисықты, осы облыстан шықпай бір нүктеге сығымдауға болса.

Кері жағдайда 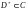облысы көпбайланысты деп аталады.

Егер D -ның шекарасы өзара қиылыспайтын қисықтардан тұрса, ондай D облысы -байланысты деп аталады. Ол көпбайланысты болып табылады.

Мысалы, С жазықтығындағы дөңгелек, жарты жазықтық бірбайланысты облыстар, ал сақинасы екібайланысты.

10.Функцияның анықтамасы. Өзара бірмәнді сәйкестік (бірбеттік функциялар). Комплекс айнымалы комплекс мәнді функцияның берілуі екі нықты айнымалы нақты мәнді функциялардың берілуімен мәндестігі. Функцияның геометриялық бейнелеулерінің тәсілдері (функцияның графигі R²*R²=R⁴жататын жиын болады).

Е жиынының әрбір элементіне Ғ жиынының бір элементіне сәйкес келетін ережені функция деп атаймыз. Егер мүмкін мәндер жиынтығынан алынған х-тің әрбір мәніне айнымалы у-тің белгілі бір мәні сәйкес келсе, онда у айнымалы шамасы х айнымалы шамасының функциясы деп аталады. Мұндай тәуелділік у=f(х) түрінде жазылады. Мұндағы х-ті тәуелсіз айнымалы (кейде аргумент) деп, ал оның өзгеру облысы (жиыны) у-тің анықталу облысы деп аталады. х-тің өзгеруіне байланысты айнымалы у-тің қабылдайтын мәндерінің жиынын у функциясының өзгеру облысы деп атайды. Функцияның жоғарыда берілген анықтамасында назар аударатын екі жағдай бар: біріншісі — аргумент х-тің өзгеру облысын көрсету, екіншісі — х пен у мәндерінің арасындағы сәйкестік ережені немесе заңды тағайындау. Егер х-тің бір мәніне у-тің бір ғана мәні сәйкес келсе, онда у-ті х-тің бір мәнді Функциясы деп, ал егер х-тің бір мәніне у-тің бірнеше мәні сәйкес келсе, онда у-ті х-тің көп мәнді Функциясы деп атайды. Айнымалы шамалар (х пен у) мәндерінің арасындағы сәйкестік ережені немесе заңды функциялық тәуелділік дейді. Функция көбінесе аналитикалық тәсіл немесе формула арқылы, кейде графиктік және таблицалық (дәл не жуық формулалармен есептелген) тәсілдерімен де беріледі. Ал, комплекс айнымалының функциясы деп комплекс санды D көпшілігінің комплекс санды G көпшілігіндегі f кескінін (бейнесін) айтады.

Дата добавления: 2015-09-03