Интеграл

жазықтығының D облысында үзіліссіз функциясы берілсін және 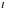- бас нүктесі ал, соңы нүктесі болатын, D облысында жатқан үзік жатық сызық болсын.

Онда комплекс айнымалы функциясынан қисыгы бойынша алынған интеграл екінші текті нақты екі қисық сызықты интеграл арқылы өрнектеледі:

,

13-теорема (Коши теоремасы). Егер функциясы, бірбайланысты D облысында аналитикалық болса, D облысында жатқан кез келген тұйық сызығы бойымен алынған интеграл нөлге тең

.

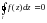14-теорема (Кошидің интегралдық формуласы). D – облысы кез келген үзік жатық тұйық сызығы шенелген болып, - осы облыста аналитикалық болсын. Онда кез келге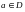н үшін

Кошидің интегралдық формуласы орынды.

15-теорема (Коши формуласы).14-теореманың шарттары орындалған жағдайда функциясының D облысында барлық ретті туындылары болады және олар

,

формулалары бойынша анықталады.

Қисық деп жолдың эквиваленттілік класстарын айтады.Егер қисық жазықтыққа қатысты үздіксіз өзгерісте болса онда бұл қисық тегіс деп аталады. Ал, егер жазықтықтағы қисық тегіс доғалардың шекті сандарынан тұрса онда, оны үзік –тегіс қисықтар деп атайды. 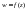деген z аргументті үзіліссіз функция берілсін және бұл комплекс жазықтығының D облысында анықталсын. Бастапқы нүктесі және соңғы нүктесі болатын, сол облыста жатқан L еркін тегіс қисықты алайық. АВ доғасын (1 сурет) ойдан алынған нүктелері арқылы n бөлікке бөлеміз, бірақ L қисығы бойымен рет ретімен орналастырамыз. Оны Қосындысын мына түрде аламыз: (1). L қисығының өлшемін деп аламыз. Белгілеу енгіземіз:

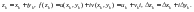
1. Формула қойып мына өрнекті аламыз:

(2)

ұмтылдырсақ (2) теңдеудің оң жағындағы 2 соңғы теңдікте шекке байланысты ұмтылады:

Бұдан барлық жекелеген доғалардың ұзындығы еркіндік заңдары бойынша 0-ге ұмтылады, ал (2) теңдіктіктің сол жағы анықталған соңғы шекке ұмтылады. Бұл шекті f(z) функциясынан L қисығы бойынша алынған интеграл деп атаймыз және деп белгілейміз. Сонда, бұл формула 2 текті қисықсызықты интеграл арқылы берілген айнымалы комплектің интегралын береді.Комплекс айнымалы интегралды шешуге келсек, онда, L қисық сызықты интегралы , түрінде берілген деп ойласақ онда,

Мұнда R(t) және I(t) нақты және жорамал бөліктері. (4) формулаға сүйенсек онда, комплекс айнымалы интегралды шешу қарапайым анықталған интегралды шешуге алып келеді.Енді интегралдың анықтамасынан шығатын қарапайым қасиеттеріне тоқталайық:

1. Интегралдың қисық бағытына тәуелділік:

2. Біртектілік:

3. Доға бойынша аддитивтілік:

L – үзік – тегіс қисық болсын, онда Олай болса,

4)Функция бойынша аддитивтілік

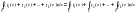
Бірбайланысты облыс үшін Коши теоремасы мен оның көпбайланысты облысқа жалпылануы.

С жазықтығындағы облыстар бірбайланысты және көпбайланысты болып бөлінеді.

А н ы қ т а м а. облысы бірбайланысты деп аталады, егер осы облыста жатқан кез келген тұйық (үзіліссіз) қисықты, осы облыстан шықпай бір нүктеге сығымдауға болса.

Кері жағдайда облысы көпбайланысты деп аталады.

Егер D -ның шекарасы өзара қиылыспайтын қисықтардан тұрса, ондай D облысы 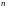-байланысты деп аталады. Ол көпбайланысты болып табылады.

Мысалы, С жазықтығындағы дөңгелек, жарты жазықтық бірбайланысты облыстар, ал сақинасы екібайланысты.

13-теорема (Коши теоремасы). Егер функциясы, бірбайланысты D облысында аналитикалық болса, D облысында жатқан кез келген тұйық сызығы бойымен алынған интеграл нөлге тең

.

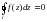23.Алғашқы функция. Алғашқы функцияның жалпы түрі. Үзіліссіз дифференциалданатын функцияның бірбайланысты облыста алғашқы функцияның бар болуы туралы теорема.Ньютон-Лейбниц формуласы.

Кошидiң интегралдық формуласы ( -дағы голоморфты функцияның G облысындағы мәндері оның шекарасындағы мәндерімен толық анықталады).

13-теорема (Коши теоремасы). Егер функциясы, бірбайланысты D облысында аналитикалық болса, D облысында жатқан кез келген тұйық сызығы бойымен алынған интеграл нөлге тең

.

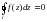14-теорема (Кошидің интегралдық формуласы). D – облысы кез келген үзік жатық тұйық сызығы шенелген болып, - осы облыста аналитикалық болсын. Онда кез келге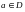н үшін

Кошидің интегралдықформуласы орынды.

15-теорема (Коши формуласы). 14-теореманың шарттары орындалған жағдайда функциясының D облысында барлық ретті туындылары болады және олар

,

формулалары бойынша анықталады

Голоморфты функцияның өз анықталы облысының әр нүктесінің маңайында Тейлор қатарымен бейнелеу туралы теорема. Коши тенсiздiгi. Лиувилль теоремасы.

20-теорема. Егер функциясы 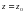нүктенін, аймағында бірмәнді аналитикалық функция

болса, онда ол осы нүктенің аймағында оң дәрежелер бойынша Тейлордың дәрежелік

қатарына жіктеледі. Бұлай жіктелгенде қатардың жинақтылық дөңгелегінің шеңбері функцияның а нүктесіне ең жақын г айырықша нүктесінен өтеді, онын, центрі а нүктесінде болады. Жинақтылық радиусы былай өрнектеледі: .

Тейлор қатарының коэффициенттері мына формулалар бойын-ша есептеліп шығарылады:

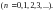
0 < r < R и n = 0,1,2,... шарты бойынша мынадай теңсіздік шығады

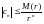, мұндағы

Дәлелдеу. Интеграл бағасы арқылы С_n көрсететін интегралды бағалайық. f функциясы тегіс бөлікті жол бойында үзіліссіз болсын γ: [α,β] → C. Онда осындай баға болады

, мұндағы

γ жолы бойында | f| фуекциясынан қисықсызықты бірінші текті интеграл бар. Көбінесе, егер

барлығы үшін

Онда , мұндағы |γ|- γ жолдың ұзындығы.

және оны поляр түрінде жазсақ . Онда

осының айғақты бөлігін алып, мынаны аламыз

Яғни әділ бағасы

Екінші пайымдау осы баға арқылы шығады өйткені

Осы қасиеттерді пайдалана,

мына теңсіздікті аламыз.

Дата добавления: 2015-09-03