Студопедия
Случайная страница | ТОМ-1 | ТОМ-2 | ТОМ-3
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатика
ИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханика
ОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторика
СоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансы
ХимияЧерчениеЭкологияЭкономикаЭлектроника

Кратные интегралы

Читайте также:
  1. Многократные оргазмы у мужчин? — Да, Да, Да!!!

Задача 1. Изменить порядок интегрирования.

1.1. 1.2.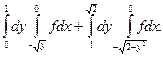
1.3. 1.4.
1.5. 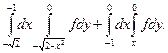1.6.
1.7. 1.8.
1.9. 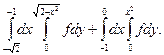1.10.
1.11. 1.12.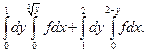
1.13. 1.14.
1.15. 1.16.
1.17. 1.18.
1.19. 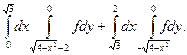1.20.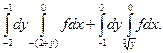
1.21. 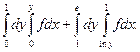1.22.
1.23. 1.24.
1.25. 1.26.
1.27. 1.28.
1.29. 1.30.

 

Задача 2. Вычислить

2.1.

2.2.

2.3.

2.4.

2.5.

2.6.

2.7.

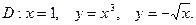
2.8.

2.9.

2.10.

2.11.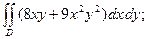

2.12.

2.13.

2.14.

2.15.

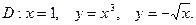
2.16.

2.17.

2.18.

2.19.

2.20.

2.21.

2.22.

2.23.

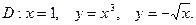
2.24.

2.25.

2.26.

2.27.

2.28.

2.29.

2.30.

Задача 3. Вычислить

3.1.

3.2.

3.3.

3.4.

3.5.

3.6.

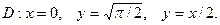
3.7.

3.8.

3.9.

3.10.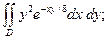

3.11.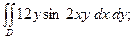

3.12.

3.13.

3.14.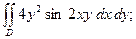

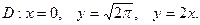
3.15.

3.16.

3.17.

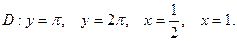
3.18.

3.19.

3.20.

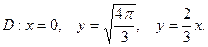
3.21.

3.22.

3.23.

3.24.

3.25.

3.26.

3.27.

3.28.

3.29.

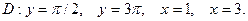
3.30.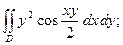

 

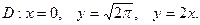
Задача 4. Вычислить

4.1.

4.2.

4.3.

4.4.

4.5.

4.6.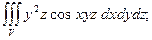

4.7.

4.8.

4.9.

4.10.

4.11.

4.12.

4.13.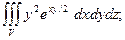

4.14.

4.15.

4.16.

4.17.

4.18.

4.19.

4.20.

4.21.

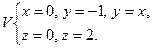
4.22.

4.23.

4.24.

4.25.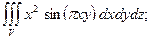

4.26.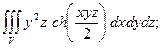

4.27.

4.28.

4.29.

4.30.

 

Задача 5. Найти площадь фигуры, ограниченной данными линиями

5.1. у = 3/х, у = 4ех, у = 3, у = 4.

5.2. х = , x = 6 - .

5.3. х2 + у2 = 72, 6у = - х2 (y£ 0).

5.4. х = 8 – y2, x = - 2y.

5.5. у = , у = 8ех, у = 3, у = 8.

5.6. у = , у = , x = 16.

5.7. x = 5 – у2, х = - 4у.

5.8. х2 + у2 = 12, - = х2 (y £ 0).

5.9. х = , у = , х = 0 (х³0).

5.10. у = , у = , x = 9.

5.11. х = , , 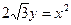х = 0 (х³ 0).

5.12. у = sinx, у = сosx, x = 0 (x³ 0).

5.13. у = 20 – x2, у = -8x.

5.14. х = , у = .

5.15. у = 32 – x2, у = -4x.

5.16. у = 2/x, y = 5ex, у = 2, у = 5.

5.17. х2 + у2 = 36, (y 0).

5.18. у = 3 , у =3/х, х = 4.

5.19. у = 6 - , у = , х = 0 (x³0).

5.20. у = 25/4 – х2, y = х – 5/2.

5.21. у = , у = 1/х, х = 16.

5.22. у = 2/x, y = 7ex, у = 2, y= 7.

5.23. у = 27 – у2, х = - 6у.

5.24. у = , 6х = у2, у = 0 (у ³ 0).

5.25. у = , у = .

5.26. у = , у = , x = 4.

5.27. у = sinx, у = сosx, x = 0 (x £ 0).

5.28. у = , у = 6ех, у = 1, у = 6.

5.29. у = 3 , у = 3/х, х = 9.

5.30. у = 11 – х2, у = - 10х.

 

Задача 6. Найти площадь фигуры, ограниченной данными линиями

6.1. у2 – 2у + х2 = 0, y2 – 4у + х2 = 0, y = х/ , у = х.
6.2. х2 – 4х + у2 = 0, х2 – 8х + у2 = 0, у = 0, у = х/ .
6.3. у2 – 6у + х2 = 0, у2 – 8у + х2 = 0, у = х/ , у = х.
6.4. х2 – 2х + у2 = 0, х2 – 4х + у2 = 0, у = 0, у = х.
6.5. у2 – 8у + х2 = 0, у2 – 10у + х2 =0, у = , у = х.
6.6. х2 – 4х + у2 = 0, х2 – 8х + у2 = 0, у = 0, у = х.
6.7. у2 – 4у + х2 = 0, у2 – 6у + х2 = 0, у = х, х = 0.
6.8. х2 – 2х + у2 = 0, х2 – 10х + у2 = 0, у = 0, у = х.
6.9. у2 – 6у + х2 = 0, у2 – 10у + х2 = 0, у = х, х = 0.
6.10. х2 – 2х + у2 = 0, х2 – 4х + у2 = 0. у = х/ , у = х.
6.11. у2 – 2у + х2 = 0, у2 – 4у + х2 = 0, у = х, х = 0.
6.12. х2 – 2х + у2 = 0, х2 – 6х + у2 = 0, у = х/ , у = х.
6.13. у2 – 4у + х2 = 0, у2 – 6у + х2 = 0, у = х, х = 0.
6.14. х2 – 2х + у2 = 0, х2 – 8х + у2 = 0, у = х/ , у = х.
6.15. у2 – 2у + х2 = 0, у2 – 6у + х2 = 0, у = х/ , х = 0.
6.16. х2 – 2х + у2 = 0, х2 – 4х + у2 = 0, у = 0, у = х/ .
6.17. у2 – 2у + х2 = 0, у2 – 10у + х2 = 0, у = х/ х, у = х.
6.18. х2 – 2х + у2 = 0, х2 – 6х + у2 = 0, у = 0, у = х/ .
6.19. у2 – 4у + х2 = 0, у2 – 10у + х2 = 0, у = х/ , у = х.
6.20. х2 – 2х + у2 = 0, х2 – 6х + у2 = 0, у = 0, у = х.
6.21. у2 – 2у + х2 = 0, у2 – 4у + х2 = 0, у = х, х = 0.
6.22. х2 – 2х + у2 = 0, х2 – 4х + у2 = 0, у = 0, у = х.
6.23. у2 – 6у + х2 = 0, у2 – 8у + х2 = 0, у = х, х = 0.
6.24. х2 – 4х + у2 = 0, х2 – 8х + у2 = 0, у = 0, у = х.
6.25. у2 – 4у + х2 = 0, у2 – 8у + х2 = 0, у = х, х = 0.
6.26. х2 – 4х + у2 = 0, х2 – 8х + у2 = 0, у = х/ , у = х.
6.27. у2 – 4у + х2 = 0, у2 – 8у + х2 = 0, у = х, х = 0.
6.28. х2 – 4х + у2 = 0, х2 – 6х + у2 = 0, у = х/ , у = х.
6.29. у2 – 2у + х2 = 0, у2 – 10у + х2 = 0, у = х/ , х = 0.
6.30. х2 – 6х + у2 = 0, х2 – 10х + у2 = 0, у = х/ , у = х.

 

Задача 7. Пластинка D задана ограничивающими ее кривыми, m - поверхностная плотность. Найти массу пластинки.

7.1. D: х = 1, у = 0, у2 = 4х (у ³ 0); m = 7х2 + у.
7.2. D: х2 + у2 = 1, х2 + у2 = 1, х = 0, у = 0 (х ³ 0, у ³ 0); m = (х + у)/(х2 + у2).
7.3. D: х = 1, у = 0, у2 = 4x (у ³ 0); m = 7х2/2 + 5у.
7.4. D: х2 + у2 = 9, х2 + у2 = 16, х = 0, у = 0 (х ³ 0, у ³ 0); m = (2х + 5у)/(х2 + у2).
7.5. D: х = 2, у = 0, у2 = 2x (у ³ 0); m = 7х2/8 + 2у.
7.6. D: х2 + у2 = 1, х2 + у2 = 16, х = 0, у = 0 (х ³ 0, у ³ 0); m = (х + у)/(х2 + у2).
7.7. D: х = 2, у = 0, у2 = x/2 (у ³ 0); m = 7х2/2 + 6у.
7.8. D: х2 + у2 = 4, х2 + у2 = 25, х = 0, у = 0 (х ³ 0, у £ 0); m = (2х - 3у)/(х2 + у2).
7.9. D: х = 1, у = 0, у2 = 4x (у ³ 0); m = х + 3у2.
7.10. D: х2 + у2 = 1, х2 + у2 = 9, х = 0, у = 0 (х ³ 0, у £ 0); m = (х - у)/(х2 + у2).
7.11. D: х = 1, у = 0, у2 = x (у ³ 0); m = 3х + 6у2.
7.12. D: х2 + у2 = 9, х2 + у2 = 25, х = 0, у = 0 (х £ 0, у ³ 0); m = (2y - x)/(х2 + у2).
7.13. D: х = 2, у = 0, у2 = x/2 (у ³ 0); m = 2х + 3у2.
7.14. D: х2 + у2 = 4, х2 + у2 = 16, х = 0, у = 0 (х £ 0, у ³ 0); m = (2y - x)/(х2 + у2).
7.15. D: х = , у = 0, у2 = 8x (у ³ 0); m = 7х + 3у2.
7.16. D: х2 + у2 = 9, х2 + у2 = 16, х = 0, у = 0 (х £ 0, у ³ 0); m = (2y - 5x)/(х2 + у2).
7.17. D: х = 1, у = 0, у2 = 4x (у ³ 0); m = 7х2 + 2у.
7.18. D: х2 + у2 = 1, х2 + у2 = 16, х = 0, у = 0 (х ³ 0, у ³ 0); m = (x + 3y)/(х2 + у2).
7.19. D: х = 2, у2 = 2x, у = 0 (у ³ 0); m = 7х2/4 + у/2.
7.20. D: х2 + у2 = 1, х2 + у2 = 4, х = 0, у = 0 (х ³ 0, у ³ 0); m = (x + 2y)/(х2 + у2).
7.21. D: х = 2, у = 0, у2 = 2x (у ³ 0); m = 7х2/4 + у.
7.22. D: х2 + у2 = 1, х2 + у2 = 9, х = 0, у = 0 (х ³ 0, у £ 0); m = (2x - y)/(х2 + у2).
7.23. D: х = 2, у = 0, у2 = x/2 (у ³ 0); m = 7х2/2 + 8у.
7.24. D: х2 + у2 = 1, х2 + у2 = 25, х = 0, у = 0 (х ³ 0, у £ 0); m = (x - 4y)/(х2 + у2).
7.25. D: х = 1, у = 0, у2 = 4x (у ³ 0); m = 6х + 3у2.
7.26. D: х2 + у2 = 4, х2 + у2 = 16, х = 0, у = 0 (х ³ 0, у £ 0); m = (3x - y)/(х2 + у2).
7.27. D: х = 2, у = 0, у2 = x/2 (у ³ 0); m = 4х + 6у2.
7.28. D: х2 + у2 = 4, х2 + у2 = 9, х = 0, у = 0 (х £ 0, у ³ 0); m = (у - 4x)/(х2 + у2).
7.29. D: х = 1/2, у = 0, у2 = 2x (у ³ 0); m = 4х + 9у2.
7.30. D: х2 + у2 = 4, х2 + у2 = 9, х = 0, у = 0 (х £ 0, у ³ 0); m = (у - 2x)/(х2 + у2).

 

Задача 8*. Найтиобъем тела, заданного ограничивающими его поверхностями.

8.1. z=0, x+z=2.

8.2. z=0, z=5+5 .

8.3. x2+y2=2, y=0, z=0, z=15x

8.4. x+y=2, z=12y, z=0

8.5. x=20 x=5 z=0, z+y=1/2

8.6. x=5 x=5y/6, z=0, z= (3+ )

8.7. x2+y2=2, x=0, z=0, z=30x

8.8. x+y=2, z=12x/5, z=0

8.9. y=17 y=2 z=0, x+z=1/2

8.10. z=0, z=5(3+ )/9.

8.11. x2+y2=8, y=0, z=0, z=15x/11

8.12. x+y=4, y= z=3y, z=0

8.13. x= x= y, z=0, z= (3+ )

8.14. x=19 x=4 z=0, z+y=2

8.15. x2+y2=8, 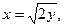x=0 z=30y/11, z=0

8.16. x+y=4, 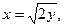z=3x/5, z=0

8.17. y=6 y= z=0, x+z=3

8.18. y= y= x, z=0, z= (3+ )

8.19. x2+y2=18, y= y=0, z=0, z=5x/11

8.20. x+y=6, y= z=4y, z=0

8.21. x=7 x=2 z=0, z+y=3

8.22. 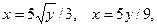z=0, z=5(3+ )/9

8.23. x2+y2=18, x= x=0, z=0, z=10/11.

8.24. x+y=6, x= x=4x/5, z=0

8.25. y= , y= x, z=0, z=

8.26. x2+y2=50, y= 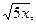y=0, z=0, z=3x/11.

8.27. x+y=8, y= z=3y, z=0

8.28. x=16 x= z+y=2 z=0,

8.29. x=15 x=15y, z=0, z=15

8.30. x2+y2=50, x= x=0, z=0, z=6y/11.

 

Задача 9*. Найти объем тела, заданного ограничивающими его поверхностями

9.1. x2+y2=2y, z=5/4- x2, z=0

9.2. x2+y2=y, z2+y2=4y, z= z=0

9.3. x2+y2=8 z=x2+y2-64, z=0, (z ≥ 0).

9.4. x2+y2+4x=0, z=8-y2, z=0

9.5. x2+y2=6x, x2+y2=9x, z= z=0, y=0, (y ≤ 0).

9.6. x2+y2=6 z=x2+y2-36, z=0, (z ≥ 0).

9.7. x2+y2=2y, z= 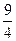-x2, z=0.

9.8. x2+y2=2y, x2+y2=5y, z= z=0.

9.9. x2+y2+2 =0, z=x2+y2-4, z=0, (z ≥ 0).

9.10. x2+y2=4x, z=10-y2, z=0.

9.11. x2+y2=7x, x2+y2=10x, z= z=0. y=0, (y ≤ 0).

9.12. x2+y2=8 , z=x2+y2-64, z=0, (z ≥ 0).

9.13. x2+y2=2y, z= 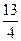-x2, z=0.

9.14. x2+y2=3y, x2+y2=6y, z= z=0.

9.15. x2+y2=6 , z=x2+y2-36, z=0, (z ≥ 0).

9.16. x2+y2=2 , z=x2+y2-4, z=0, (z ≥ 0).

9.17. x2+y2=4x, z=12 - y2, z=0.

9.18. x2+y2=8x, x2+y2=11x, z= z=0. y=0, (y ≤ 0).

9.19. x2+y2=4 , z=x2+y2-16, z=0, (z ≥ 0).

9.20. x2+y2=4y, z=4 - x2, z=0.

9.21. x2+y2=4y, x2+y2=7y, z= z=0.

9.22. x2+y2=4 , z=x2+y2-16, z=0, (z ≥ 0).

9.23. x2+y2+2x=0, z=17/4- y2, z=0.

9.24. x2+y2=9x, x2+y2=12x, z= z=0. y=0, (y ≥ 0).

9.25. х2 + у2 + 2 = 0, z = х2 + у2 – 4, z = 0, (z ³ 0).

9.26. х2 + у2 = 4у, z = 6 - х, z = 0.

9.27. х2 + у2 = 10x, х2 + у2 = 13x, z = 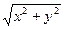, z = 0, y = 0 (y ³ 0).

9.28. х2 + у2 = 2 , z = х2 + у2 – 4, z = 0, (z ³ 0).

9.29. х2 + у2 = 2x, z = 21/4 - у2, z = 0.

9.30. х2 + у2 = 5y, х2 + у2 = 8y, z = 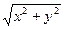, z = 0.

Задача 10*. Найти объем тела, заданного ограничивающими его поверхностями

10.1. у = 5х2 + 2, у = 7, z = 3у2 - 7х2 - 2, z = 3у2 - 7х2 – 5.

10.2. у = 5х2 - 2, у = -4х2 + 7, z = 4+ 9х2 + 5у2, z = -1 + 9х2 + 5у2.

10.3. у = -5у2 + 2, х = -3, z = 3х2 + у2 + 1, z = 3х2 + 3у2 – 5.

10.4. у = 2у2 - 3, х = -7у2 + 6, z = 1 + , z = -3 + .

10.5. у = -6х2 + 8, у = 2, z = х – х2 - у2 - 1, z = х – х2 - у2 - 5.

10.6. у = 5х2 - 1, у = -3х2 + 1, z = -2 + , z = -5 + .

10.7. х = 5у2 - 9, х = -4, z = х2 + 4х - у2 - 4, z = х2 + 4х - у2 + 2.

10.8. у = 6х2 - 1, у = 5, z = 2х2 + х - у2 , z = 2х2 + х - у2 + 4.

10.9. х = 5у2 - 1, х = -3у2 + 1, z = 2 - , z = -1 - .

10.10. х = -3у2 + 7, х = 4, z = 2 + 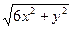, z = 3 + .

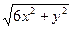10.11. у = -5х2 + 3, у = -2, z = 2х2 – 3у - 6у2 - 1, z = 2х2 - 3у - 6у2 + 2.

10.12. у = х2 - 5, у = -х2 + 3, z = 4 + , z = 1 + .

10.13. х = 3у2 - 5, х = -2, z = 2 - , z = 8 - .

10.14. х = у2 - 2, х = -4у2 + 3, z = + 2, z = - 1.

10.15. у = 2х2 - 1, у = 1, z = х2 – 5у2 - 3, z = х2 - 5у2 - 6.

10.16. у = х2 - 2, у = -4х2 + 3, z = 2 + 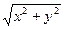, z = -1 + .

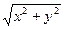10.17. х = -4у2 + 1, х = -3, z = х2 - 7у2 - 1, z = х2 - 7у2 + 2.

10.18. х = 7у2 - 6, х = -2у2 + 3, z = 3 + 5х2 - 8у2, z = -2 + 5х2 - 8у2.

10.19. у = 1 - 2х2, у = - 1, z = х2 + 2у + у2 - 2, z = х2 + 2у + у2 + 1.

10.20. у = х2 - 7, у = -8х2 + 2, z = 3 – 12у2 + 5х2, z = -2 – 12у2 + 5х2.

10.21. х = 2у2 + 3, х = 5, z = 1 + 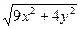, z = 4 + .

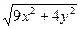10.22. у = 3х2 + 4, у = 7, z = 5 - , z = 1 - .

10.23. х = 5у2 -27, z = 4 - , z = -1 - .

10.24. х = -2у2 + 5, х = 3, z = 5 - 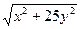, z = 2 - .

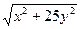10.25. у = -3х2 + 5, у = 2, z = 3 + , z = -1 + .

10.26. у = 3х2 - 5, у = -6х2 + 4, z = 2 + 10х2 - у2, z = -2 + 10х2 - у2.

10.27. х = 4у2 + 2, х = 6, z = х2 + 4у2 +у + 1, z = х2 + 4у2 +у + 4.

10.28. х = 3у2 - 2, х = -4у2 + 5, z = 4 - 7х2 - 9у2, z = 1 - 7х2 - 9у2.

10.29. у = 2х2 - 5, у = -3, z = 2 + , z = -1 + .

10.30. у = 2х2 - 3, у = -7х2 + 6, z = 1 - 5х2 - 6у2, z = -3 - 5х2 - 6у2.

 

Список литературы

  1. Бугров Я.С., Никольский С.М. Высшая математика. Том I,II «Дрофа», Москва, 2004.
  2. Ильин В.А., Куркина А.В. Высшая математика. «Проспект», Москва,2005.
  3. Данко П.Е., Попова А.Г., Кожевникова Т.Я. Высшая математика упражнениях и задачах. Том I,II «Высшая школа», Москва, 1999.
  4. Сборник задач по курсу высшей математике под редакцией Крючковича Г.И. «Высшая математика», Москва, 1973.
  5. Бронштейн И.Н., Семендяев К.А. Справочник по математике. «Наука», Москва, 1981.

 

Дата добавления: 2015-09-03; просмотров: 56 | Нарушение авторских прав

<== предыдущая страница | следующая страница ==>
В А Р И А Н Т 30| Требования к представлению работы
mybiblioteka.su - 2015-2024 год. (0.066 сек.)