
Теорема. f функциясы еркін облыста D ⊂C голоморфты, D-да голоморфты болатын барлық реттегі туындысы бар. Тейлор қатарының n-ші туындысы f (n)(z) еркін нүктесінде a ∈D n-еселенген Тейлор қатарының f(z) үшін дифференциалдануы д.а.
Дәлелдеу. Тейлор қатарының f(z) үшін центрі а болатын нүктедегі UR(a) дөңгелек жинақтылығын қарастырайық. Демек, f’ функциясы UR(a) дөңгелегінде голоморфты,ал оның табыстаушы қатары центрі а болатын функция Тейлор қатары болып табылады. f’ үшін бұл пайымдауды қайталай келе,. f’’ ’үшін дәл сондай пайымдау аламыз. Нүктенің туындылау a ∈D күшіне f функциясы D-да барлық реттегі туындысы бар болады.
Морера теоремасы Кошидің интегралдық теоремасының толық емес айналымы болып табылады және комплексті айнымалы функциялар теориясының негізгі теорияларының бірі болып табылады. Ол былай тұжырымдалады:
Егер  комплексті айнымалы z функциясы D облысында үзіліссіз және интеграл одан барлық тұйық контур бойынша γ
комплексті айнымалы z функциясы D облысында үзіліссіз және интеграл одан барлық тұйық контур бойынша γ  D нөлге тең,яғни
D нөлге тең,яғни

Мұндағы  - Dоблысындағы аналитикалық функция.
- Dоблысындағы аналитикалық функция.
D облысында жататын шекара бойынша алынған кез келген үшбұрыштың интергалдарын нөлге айналу талабымен шектеліп теорема шартын жеңілдетуге де болады.
Морера теоремасы қиын анықталатын кейбір функцияларды аналитикалық екенін дәлелдеу болып табылады. Егер  аналитикалық функцияның реттілігі біркелкі
аналитикалық функцияның реттілігі біркелкі 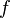 функциясымен дәл келеді,онда
функциясымен дәл келеді,онда

Сол себепті, Морера теоремасы бойынша шекті функция голоморфты болады. Осылайша көп функцияның голоморфтылығы дәлелденеді,мысалы Риман дзета-функциясы арқылы есептелінген:

Және Эйлердің гамма-функциясы арқылы

Морера теоремасы симметрия принципі бойынша бекітілген функцияның аналитикалық екенін дәлелдеу үшін қолданылады.
Лоран катары, оның жинақталу облысы. Сақинаның ішінде голоморфты функцияны Лоран қатарына жiктеу.
Дөңгелек ішінде аналитикалық функцияның Тейлор қатарына жіктелетінін көрдік. Көпшілік жағдайда  нүктесінің өзінен басқа, ол нүктенің маңайындағы аналитикалық функцияларды қарастыруға тура келеді. Яғни,
нүктесінің өзінен басқа, ол нүктенің маңайындағы аналитикалық функцияларды қарастыруға тура келеді. Яғни,  функциясы
функциясы 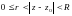 сақинада аналитикалық болсын. Осы функцияны көрсетілген облыста жіктеуде алынған қатар Лоран қатары деп аталады.
сақинада аналитикалық болсын. Осы функцияны көрсетілген облыста жіктеуде алынған қатар Лоран қатары деп аталады.
22-теорема (Лоран теоремасы). Егер  функциясы
функциясы 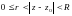 сақина ішінде бірмәнді аналитикалық функция болса, онда ол осы сақинаның ішінде мына Лоран қатарына жіктеледі:
сақина ішінде бірмәнді аналитикалық функция болса, онда ол осы сақинаның ішінде мына Лоран қатарына жіктеледі:
 , (5)
, (5)
Бұл қатарда  айырманың оң дәрежелері де, теріс дәрежелері де бар.
айырманың оң дәрежелері де, теріс дәрежелері де бар.
Лоран қатарының коэфициенттері жалпы түрдекелесі формуламен анықталады:
 , (6)
, (6)
мұндағы  сызығы
сызығы  нүктесін қамтитын
нүктесін қамтитын 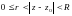 сақинда жатқан кез келген тұйық сызық.
сақинда жатқан кез келген тұйық сызық.


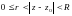 сақинасында абсолют жинақты болады.
сақинасында абсолют жинақты болады.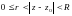 сақинасының ішінде жататын кез келген
сақинасының ішінде жататын кез келген  тұйық сақинасында абсолют және бірқалыпты жинақты болады.
тұйық сақинасында абсолют және бірқалыпты жинақты болады. функциясы
функциясы  сақинасында
сақинасында қатарына жіктелсе, онда
қатарына жіктелсе, онда  коэффиценттері (6) формуламен анықталады.
коэффиценттері (6) формуламен анықталады.
Голоморфты функциялардың оңашаланған нүктелерi. Олардың Лоран қатары негізінде классификациялау. Жөнделетін оқшауланған ерекше нүкте болу критерийі. Полюс болукритериі, Сохоцкий теоремасы.  функциясы
функциясы  нүктесінің ойылған
нүктесінің ойылған  маңайында регулярлы аналитикалық функция болсын, яғни,
маңайында регулярлы аналитикалық функция болсын, яғни,  функциясы
функциясы  нүктесінде не аналитикалық емес, не анықталмаған. Осындай
нүктесінде не аналитикалық емес, не анықталмаған. Осындай  нүктесі оңашаланған айрықша нүкте деп аталады. Егер (5) қатардың бас бөлігінің барлық
нүктесі оңашаланған айрықша нүкте деп аталады. Егер (5) қатардың бас бөлігінің барлық  коэффиценттері нөлге тең болса, онда
коэффиценттері нөлге тең болса, онда  нүктесі жөнделетінайрықша нүкте деп аталады. Бұл жағдайда
нүктесі жөнделетінайрықша нүкте деп аталады. Бұл жағдайда  болғанда
болғанда
 болады.
болады.
23-теорема.  функциясы
функциясы  нүктесінің ойылған
нүктесінің ойылған  маңайында регулярлы функция болсын. Онда
маңайында регулярлы функция болсын. Онда  нүктесі
нүктесі  функциясының жөнделетін айрықша нүктесі болуы үшін
функциясының жөнделетін айрықша нүктесі болуы үшін  шегінің бар болуы қажетті және жеткілікті.Егер (5) қатардың бас бөлігіндегі нөлден өзге
шегінің бар болуы қажетті және жеткілікті.Егер (5) қатардың бас бөлігіндегі нөлден өзге  коэффиценттерінің саны ақырлы болса, онда
коэффиценттерінің саны ақырлы болса, онда  оңашаланған айрықша нүктесі полюсом деп аталады. Бұл жағдайда
оңашаланған айрықша нүктесі полюсом деп аталады. Бұл жағдайда  болғанда
болғанда
 болады. Осы жіктеудегі
болады. Осы жіктеудегі  айырымының ең кіші дәрежесі
айырымының ең кіші дәрежесі  болады.
болады.  саны полюстің реті (немесе еселігі) деп аталады. Бірінші ретті полюс жай полюс деп аталады.
саны полюстің реті (немесе еселігі) деп аталады. Бірінші ретті полюс жай полюс деп аталады.
25-теорема.  функциясы
функциясы  нүктесінің ойылған
нүктесінің ойылған  маңайында регулярлы функция болсын. Онда
маңайында регулярлы функция болсын. Онда  нүктесі
нүктесі  функциясының полюсі болуы үшін
функциясының полюсі болуы үшін  болуы қажетті және жеткілікті.
болуы қажетті және жеткілікті.
26-теорема (Сохоцкий теоремасы). Егер  -
-  функциясының елеулі айрықша нүктесі болса, онда кез келген
функциясының елеулі айрықша нүктесі болса, онда кез келген  комплекс саны үшін,
комплекс саны үшін,  қоса есептегенде,
қоса есептегенде,  нүктесіне жинақталатын
нүктесіне жинақталатын  тізбегі табылып,
тізбегі табылып,  болады.
болады.
А н ы қ т а м а. 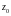 нүктесі
нүктесі  аналитикалық функциясының оңашаланған айрықша нүктесі болса, онда
аналитикалық функциясының оңашаланған айрықша нүктесі болса, онда
 , (7)
, (7)
интегралының мәнін функцияның айрықша 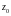 нүктесі бойынша алынған қалындысы деп атайды.
нүктесі бойынша алынған қалындысы деп атайды.
Мұндағы  -
-  нүктесін қамтитын, одан өзге айрықша нүктелерді қамтымайтын контур.Коши теоремасы бойынша, барлық осындай
нүктесін қамтитын, одан өзге айрықша нүктелерді қамтымайтын контур.Коши теоремасы бойынша, барлық осындай  контулары үшін (7) интегралдың мәні бірдей.
контулары үшін (7) интегралдың мәні бірдей.
Аналитикалық функцияның шексіз аластатылған нүкте маңайында өзгеру тәртібі. Шексіз аластатылған жөнделетін оқшауланған, полюс, айрықша оқшауланған нүкте болуы.
Е жиынының әрбір элементіне Ғ жиынының бір элементіне сәйкес келетін ережені функция деп атаймыз.  функциясы
функциясы  нүктесінің ойылған
нүктесінің ойылған  маңайында регулярлы аналитикалық функция болсын, яғни,
маңайында регулярлы аналитикалық функция болсын, яғни,  функциясы
функциясы  нүктесінде не аналитикалық емес, не анықталмаған. Осындай
нүктесінде не аналитикалық емес, не анықталмаған. Осындай  нүктесі оңашаланған айрықша нүкте деп аталады. Егер (5) қатардың бас бөлігінің барлық
нүктесі оңашаланған айрықша нүкте деп аталады. Егер (5) қатардың бас бөлігінің барлық  коэффиценттері нөлге тең болса, онда
коэффиценттері нөлге тең болса, онда  нүктесі жөнделетінайрықша нүкте деп аталады. Бұл жағдайда
нүктесі жөнделетінайрықша нүкте деп аталады. Бұл жағдайда  болғанда
болғанда
 болады.
болады.
23-теорема.  функциясы
функциясы  нүктесінің ойылған
нүктесінің ойылған  маңайында регулярлы функция болсын. Онда
маңайында регулярлы функция болсын. Онда  нүктесі
нүктесі  функциясының жөнделетін айрықша нүктесі болуы үшін
функциясының жөнделетін айрықша нүктесі болуы үшін 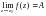 шегінің бар болуы қажетті және жеткілікті. Егер (5) қатардың бас бөлігіндегі нөлден өзге
шегінің бар болуы қажетті және жеткілікті. Егер (5) қатардың бас бөлігіндегі нөлден өзге  коэффиценттерінің саны ақырлы болса, онда
коэффиценттерінің саны ақырлы болса, онда  оңашаланған айрықша нүктесі полюсом деп аталады. Бұл жағдайда
оңашаланған айрықша нүктесі полюсом деп аталады. Бұл жағдайда  болғанда
болғанда
 болады.
болады.
Осы жіктеудегі  айырымының ең кіші дәрежесі
айырымының ең кіші дәрежесі  болады.
болады.  саны полюстің реті (немесе еселігі) деп аталады. Бірінші ретті полюс жай полюс деп аталады.
саны полюстің реті (немесе еселігі) деп аталады. Бірінші ретті полюс жай полюс деп аталады.
24-теорема.  нүктесі
нүктесі  функциясының
функциясының  -шы ретті полюсі болуы үшін ол нүктенің
-шы ретті полюсі болуы үшін ол нүктенің  функциясының
функциясының  -шы ретті нөлі болуы қажетті және жеткілікті.
-шы ретті нөлі болуы қажетті және жеткілікті.
25-теорема.  функциясы
функциясы  нүктесінің ойылған
нүктесінің ойылған  маңайында регулярлы функция болсын. Онда
маңайында регулярлы функция болсын. Онда  нүктесі
нүктесі  функциясының полюсі болуы үшін
функциясының полюсі болуы үшін  болуы қажетті және жеткілікті.Егер (5) қатардың бас бөлігіндегі нөлден өзге
болуы қажетті және жеткілікті.Егер (5) қатардың бас бөлігіндегі нөлден өзге  коэффиценттерінің саны ақырсыз (шексіз) болса, онда
коэффиценттерінің саны ақырсыз (шексіз) болса, онда  елеулі айрықша нүкте деп аталады. Функцияның елеулі айырықша нүкте аймағындағы айтарлықтай толық сипаттамасын Сохоцкий теоремасы баяндайды.
елеулі айрықша нүкте деп аталады. Функцияның елеулі айырықша нүкте аймағындағы айтарлықтай толық сипаттамасын Сохоцкий теоремасы баяндайды.
26-теорема (Сохоцкий теоремасы). Егер  -
-  функциясының елеулі айрықша нүктесі болса, онда кез келген
функциясының елеулі айрықша нүктесі болса, онда кез келген  комплекс саны үшін,
комплекс саны үшін,  қоса есептегенде,
қоса есептегенде,  нүктесіне жинақталатын
нүктесіне жинақталатын  тізбегі табылып,
тізбегі табылып,  болады.
болады.
А н ы қ т а м а.  нүктесі
нүктесі  аналитикалық функциясының оңашаланған айрықша нүктесі болса, онда
аналитикалық функциясының оңашаланған айрықша нүктесі болса, онда
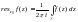 , (7)
, (7)
интегралының мәнін функцияның айрықша  нү итктесі бойынша алынған қалындысы деп атайды.Мұндағы
нү итктесі бойынша алынған қалындысы деп атайды.Мұндағы 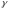 -
-  нүктесін қамтитын, одан өзге айрықша нүктелерді қамтымайтын контур.Коши теоремасы бойынша, барлық осындай
нүктесін қамтитын, одан өзге айрықша нүктелерді қамтымайтын контур.Коши теоремасы бойынша, барлық осындай  контулары үшін (7) интегралдың мәні бірдей.
контулары үшін (7) интегралдың мәні бірдей.
30.Қалындылар. Қалындыны жай полюсте, ақырлы ерекше нүктелерде, еселі полюсте есептеу.
Қалындылар туралы негізгі теорема. Меншіксіз интегралдарды қалындар көмегімен есептеу.
27-теорема (қалындылар туралы теорема). Егер  функциясының
функциясының  контурының ішінде
контурының ішінде  оңашаланған айрықша нүктелері болса, онда
оңашаланған айрықша нүктелері болса, онда 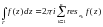 теңдігі орындалады.
теңдігі орындалады.
28-теорема. Бірмәнді оңашаланған айрықша  нүктесіндегі қалынды
нүктесіндегі қалынды  функциясының
функциясының  дегі Лоран қатарының
дегі Лоран қатарының  коэффицентіне тең, яғни
коэффицентіне тең, яғни
 .
.
29-теорема.  -
-  функциясының жай полюсі болсын.
функциясының жай полюсі болсын.  және
және  . Онда
. Онда  -тің
-тің  нүктедегі қалындысы келесідей анықталады:
нүктедегі қалындысы келесідей анықталады:
 .
.
30-теорема.  -
-  функциясының
функциясының  ретті полюсі болсын. Онда
ретті полюсі болсын. Онда  -тің
-тің  нүктедегі қалындысы келесідей анықталады:
нүктедегі қалындысы келесідей анықталады:
 .
.
А н ы қ т а м а.  функциясының
функциясының 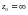 нүктедегі қалындысы деп Лоран қатарындағы бірінші теріс дәреженің қарама-қарсы таңбамен алынған коэффицентін атайды, яғни
нүктедегі қалындысы деп Лоран қатарындағы бірінші теріс дәреженің қарама-қарсы таңбамен алынған коэффицентін атайды, яғни  .
.
Дата добавления: 2015-09-03; просмотров: 442 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Луивилль теоремасы | | | Однокомнатная квартира в самом центре Севастополя (ул. Генерала Петрова). Шифр: 1/01 |