Облыс пен шекара

Комплекс сандар анықтамасы. Комплекс сандарға қолданылатын алгебралық амалдар мен олардың қасиеттері. Кез келген комплекс санды...

Комплекс сандар анықтамасы. Комплекс сандарға қолданылатын алгебралық амалдар мен олардың қасиеттері. Кез келген комплекс санды түрінде жазуға болатындығы алгебра курсынан белгілі, мұндағы және – кез келген нақты сандар, ал -жорамал бірлік..

саны комплекс санның нақты бөлігі деп аталып арқылы белгіленеді, жорамал бөлігі деп аталып – 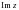арқылы белгіленеді.

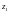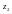және комплекс сандары тең деп аталады сол жағдайда,тек қана сол жағдайдаегер 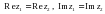болса.

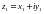және комплекс сандарының қосындысы деп 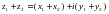комплекс санын атайды.

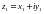және комплекс сандарының көбейтіндісі деп комплекс санын атайды.

Көбейтіндінің қасиеттері: 1) z₁*z₂=z₂*z_1. 2) (z₁*z₂)z₃=z₁(z₂+z₃). 3)(1+0i)z=z; (a+ib)(1+i0)=a+ib. 4) z*z``=1.

z``=1/z=z^-1.

Сонымен, комплекс сандарын қосу мен көбейту, 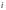символна қатысты көпмүшеліктерге амалдар қолданғандағыдай.

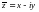саны санына түйіндес сан деп аталады.

Комплекс сандарды қосу мен көбейтуамалдары коммутативтік, ассоциативтік жәнедистрибутивтік заңдарға бағынатынына көз жеткізу қиын емес, яғни

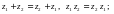
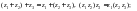
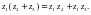
Комплекс жазықтығы комплекс сандар жиынын геометриялық бейнелеу ретінде. Комплекс санның модулi мен аргументi, қасиеттері; комплекс санның жазылуыныңтригонометриялық түрi.

D – комплекс жазықтығында берілген облыс болсын (z комплекс сандардың жиыны). Егер әрбір нүктесіне қандай да бір заңдылықпен бір ғана 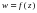комплек саны сәйкестендірілсе, онда D облысында z комплекс айнымалының бірмәнді 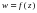функциясы анықталған дейді. Е жиынының әрбір элементіне Ғ жиынының бір элементіне сәйкес келетін ережені функция деп атаймыз.

Комплекс айнымалының 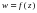функциясын геометриялық тұрғыда қарастыру үшін жазықтығымен қатар нақты бөлігі u, ал жорамалбөлігі v болатын, комплекс айнымалының екінші жазықтығын қарастыру қажет. 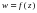функциясы әрбір нүктесіне нүктесін сәйкес қояды. z нүктесі D облысында өзгергенде оған сәйкес w нүктесі облысындағы мәндерді қабылдайды.

Сонымен, комплекс айнымалының 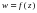функциясы, геометриялық тұрғыда, D облысын облысына бейнелейді.

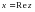, болсын. шамасы комплекс санның модулі деп аталып, символымен белгіленеді. теңдіктерін қанағаттандыратын кез келген 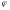саны, комплекс санның аргументі деп аталып, символымен белгіленеді. шамасы тек қана нөлден өзге комплекс сандар үшін анықталады. -тің кез келген екі мәнінің айрымы -ге еселі болады.

Кез кеген комплекс санын тригонометриялық түрде өрнектеуге болады, мұндағы .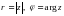

Комплекс сандарды натурал дәрежеге шығару, Муавр формуласы. Комплекс санның n-ші ретті түбірі. Дәрежелік функция , мұндағы - натурал сан.

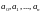Дәрежелік функциялар арқылы комплекс айнымалы -тен тәуелді көпмүшеліктер (немесе полиномдар) құрастыруға болады: , коэффиценттрі - кез келген комплекс сандар

- комплекс санның көрсеткіштік түрде жазылуы.Кез келген натурал үшін дәрежесі Муавр формуласы арқылы өрнектеледі. комплекс санның ші дәрежелі түбірі, әртүрлі мәнге ие болады. Олар келесі формула арқылы анықталады:

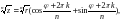
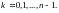
Көп жағдайда комплекс санды жазықтықтағы нүктелер бейнелеген ыңғайлы (немесе векторлармен). Әрбір , , 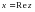, комплекс саннына абсцисасы және ординатасы

болатын 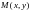нүктесі немесе ОМ векторы сәйкес келтіріледі. Векторларды қосу сәйкес комплекс сандарды қосуды білдірелі.

Комплекс сандар бейнеленген жазықтық комплекс жазықтық деп, Х– осі нақты ось, ал У – жорамал ось деп аталады.

Ақырлы комплексжазықтық С арқылы белгіленеді.

С және маңайлары. С және топология. С және ойылған маңайлар. С және жиындардың ішкі, шектік, шекаралық және сыртқы нүктелері, ашық және тұйық жиындар (С және ).

Облыс пен шекара

Комплекс жазықтықтың 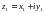және 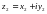нүктелерінің ара қашықтығы аналитикалық геометриядан белгілі

(1)

формуламен анықталады.

Басқаша айтқанда, (1) формула жазықтығында метриканы анықтайды.

Егер оң саны бекітілген болса, онда 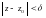теңсіздігін қанағаттандыратын нүктелер жиыны, zкомплексжазықтығындарадиусы , ал центрі нүктесіндегі дөңгелектің ішкі нүктелері болады. Ол нүктесінің -маңайы деп аталады.

нүктесі D жиынының ішкі нүктесі деп аталады, егер D жиыныда нүктесімен бірге

оның қандай бір маңайы жатса.

А н ы қ т а м а. Жазықтықтағы нүктелердің D жиыны ашық деп аталады, егер нүктелерінің барлығы D жиынының ішкі нүктелері болса.

Мысалы, сақинасы ашық жиын.

А н ы қ т а м а. Ашық D жиыны облыс деп аталады, егер ол байланысты болса, яғни кез келген нүктелерін толығымен D –да жататын 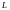сызығымен жалғауға болса.

Мысалы, жиыны облыс.

Екі дөңгелек и нүктелерінен тұратын D жиыны ашық, бірақ байланысты емес. Мысалы, осы шеңберлер ценрі болатын -1 және +1 нүктелерін барлық нүктелері D да жататын, 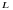қисығымен қоса алмаймыз.

А н ы қ т а м а. нүктесі D жиынының шектік нүктесі деп аталады, егер оның кез келген маңайында D жиынының ден өзге нүктелері жатса.

Барлық шектік нүктесі жиынға тиісті болса, ондай жиын тұйық деп аталады.

Ашық жиынның әрбір нүктесі сол жиынның шектік нүктесі болады. Ашық D жиынының шектік нүктесі ол жиында жатпауы да мүмкін. Онда ол D жиынының шекаралық нүктесі деп аталады.

Мысалы, болатын кез келген нүктесі жиынының шектік нүктесі.

А н ы қ т а м а. Ашық жиынның барлық шектік нүктелерінің жиынтығы оның шекарасы деп аталады.

Мысалы, сақинасының шекарасы и шеңберлер болады. Тұйық сақина 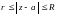теңсіздіктерімен анықталады.

С жазықтығындағы облыстар бірбайланысты және көпбайланысты болып бөлінеді.

А н ы қ т а м а. облысы бірбайланысты деп аталады, егер осы облыста жатқан кез келген тұйық (үзіліссіз) қисықты, осы облыстан шықпай бір нүктеге сығымдауға болса.

Кері жағдайда облысы көпбайланысты деп аталады.

Егер D -ның шекарасы өзара қиылыспайтын қисықтардан тұрса, ондай D облысы -байланысты деп аталады. Ол көпбайланысты болып табылады.

Мысалы, С жазықтығындағыдөңгелек, жарты жазықтық бірбайланысты облыстар, ал сақинасы екібайланысты.

А н ы қ т а м а. Шенелген жиын – табылған саннан төмен болса жоғарыдан шенелген, ал егер табылған саннан жоғары болса төменнен шенелген.

Жазықтықтың D нүктелер жиыны шенелген деп аталады, егер 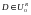болатындай дөңгелегі бар болса.

Мысалы, дөңгелегі шенелген жиын. Себебі, болғанда болады. Жоғарғы жарты жазықтық 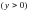шенелмеген жиын.

5. С-дағы (және -дағы) тізбектер. Олардың жинақталуы. С-дағы тізбектің жинақталуы мен екі нақты мәнді тізбектердің жинақталуымен байланысы.

6.Комплекс сандар тізбегі, С-дағы тізбектің жинақталуы мен екі нақты мәнді тізбектердің жинақталуымен байланысы. Жинақталатын тізбектердің қасиеттері. Тізбек шегінің геометриялық мағынасы.

Дата добавления: 2015-09-03