
|
Читайте также: |
Егер 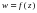 функцясы аналитикалық функция болса және D облысының бір г0 нүктесінде оның
функцясы аналитикалық функция болса және D облысының бір г0 нүктесінде оның  туындысы нольден өзгеше болса, онда г0 нүктесінің жсткілікті түрде алынған шағын аймағы
туындысы нольден өзгеше болса, онда г0 нүктесінің жсткілікті түрде алынған шағын аймағы  ) нүктені қамтитын
) нүктені қамтитын  жазықтығының бір облысына өзара бірмәнді және үздіксіз болып бейнеленеді. Бұлай бейнеленгенде
жазықтығының бір облысына өзара бірмәнді және үздіксіз болып бейнеленеді. Бұлай бейнеленгенде  нүктесінен өтетін екі қисықтың арасындағы бүрыш өзінің шамасы бойынша да, бағыты бойынша да әлгі қистықтардың
нүктесінен өтетін екі қисықтың арасындағы бүрыш өзінің шамасы бойынша да, бағыты бойынша да әлгі қистықтардың  жазықтығындағы кескіндерінің арасындағы бұрышқа дәл келеді, ал бейнелердін
жазықтығындағы кескіндерінің арасындағы бұрышқа дәл келеді, ал бейнелердін  нүктесіндегі сызықтық масштабы сол
нүктесіндегі сызықтық масштабы сол  нүктесіненөтетін қисықтардың бәріне бірдей болады.
нүктесіненөтетін қисықтардың бәріне бірдей болады.
А н ы қ т а м а. Бұрыштың шамасын да, бағытын да өзгертпейтін және керу шамасы тұрақты болатын бейнелеу конформды бейнелеу деп аталады.
Конформдық бейнелеу теориясының негізіне төмендегі теоремалар жатады.
10-теорема. Туындысы нольден өзгеше, яғни  болатын барлык, z нүктелерде
болатын барлык, z нүктелерде 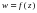 аналитикалық функция арқылы жүзеге асырылатын бейнелеу конформдық бейнелеу болады жәнебұл бейнелеуде
аналитикалық функция арқылы жүзеге асырылатын бейнелеу конформдық бейнелеу болады жәнебұл бейнелеуде  бұрылыс бұрышы болады, ал
бұрылыс бұрышы болады, ал  шамасы
шамасы  нүктелерін
нүктелерін  жазықтығының нүктелеріне бейнелегендегі созу коэффициенті болады.
жазықтығының нүктелеріне бейнелегендегі созу коэффициенті болады.
11-теорема. Z жазықтығының, толық жазықтықтан немесе бір нүктесі шығарылып тасталған
жазықтықтан өзгеше, бір бір жүйелі D облысын  жазьщтығының бір ғана дөңгелегіне өзара
жазьщтығының бір ғана дөңгелегіне өзара
бірмәнді және конформды түрде сансыз көп тәсілдермен бейнелеуге болады.
Еғер D облысының берілген  нүктесі мен сондағы бір белгілі бағыт деңгелек ішіндегі бір
нүктесі мен сондағы бір белгілі бағыт деңгелек ішіндегі бір
тиянақты нүкте мен бағытқа көшетіндей етіп сайлап алатын болсак, онда D облысы жоғарыда
айтылған дөң-гелекке бірмәнді түрде бейнеленеді.
12-теорема. Егер бірбайланысты облыстың шекарасы екі еселік нүктелері жоқ үздіксіз қисық
болса, онда облыстың дөңгелекке конформдық бейнеленуіндегі сәйкесгік шекараларға шейін өзара
бірмәнді болады.
Функционалдық қатарлар. Жинақталу нүктесі, жинақталу жиыны. Нүктелі және бірқалыпты жинақталу. Функционалдық қатардың жинакталуының Вейерштрасс белгісі. Бірқалыпты жинақталатын функциялық қатарлардың қасиеттері.
Комплекс облыстағы қатарлар теориясы математикалық анализ курсындағы қатарлар теориясы сияқты құрылады.
Мүшелері  комплекссандар болатын
комплекссандар болатын
 , (1)
, (1)
қатары берісін.
 , қатар мүшелері, ал
, қатар мүшелері, ал  —қатардың жалпы мүшесі деп аталады.
—қатардың жалпы мүшесі деп аталады.

қосындыларын қатардың дербес қосындылары деп атайды.
А н ы қ т а м а. Егер  сандық тізбегінің S -қа тең шегі бар болса, онда (1) қатары жинақталады, S саны (1) қатарының қосындысы дейді.
сандық тізбегінің S -қа тең шегі бар болса, онда (1) қатары жинақталады, S саны (1) қатарының қосындысы дейді.
Бұл жағдайда «(1) қатары S санына жинақталады» деп те атайды. Қалған жағдайлардың әрқасысында, яғни  тізбегінің
тізбегінің  ,
,  не
не  ақырсыз шектері бар не ешқандай да шегі болмағанда, (1) қатары жинақталмайды, не жинақсыз дейді.
ақырсыз шектері бар не ешқандай да шегі болмағанда, (1) қатары жинақталмайды, не жинақсыз дейді.
16-теорема (Қатар жинақтылығының қажетті шарты).
Егер  қатары жинақталса, онда оның, жалпымүшесініңшегібаржәненольгетең,яғни,
қатары жинақталса, онда оның, жалпымүшесініңшегібаржәненольгетең,яғни,  .
.
Салдар(қатаржинақталмауыныңжеткіліктішарты). Егерқатардың.жалпымүшесінольгеұмтылмаса, ондақатаржинақталмайды.
Е.скерту.  шартықатаржинақталуыныңқажеттішартыболатұрып, жеткіліктішартыемес: қатардыңжалпымүшесінольгеүмтылсада, қатаржииақталмауымүмкін.
шартықатаржинақталуыныңқажеттішартыболатұрып, жеткіліктішартыемес: қатардыңжалпымүшесінольгеүмтылсада, қатаржииақталмауымүмкін.
Теорема17. Мүшелері  комплекс сандар болатын
комплекс сандар болатын  қатары жинақталуы үшін, оның нақты және жорамал бөліктері болатын
қатары жинақталуы үшін, оның нақты және жорамал бөліктері болатын  және
және  қатарларының жинақталы қажетті және жеткілікті.
қатарларының жинақталы қажетті және жеткілікті.
Анықтама. (1) қатар абсолютжинақты деп аталады, егер оның мүшелерінің модульдерінен тұратын  қатары жинақты болса.
қатары жинақты болса.
Салыстыру белгісі. Егер барлық  үшін
үшін  болса онда
болса онда  жинақтылығынан
жинақтылығынан 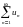 жинақтылығы шығады.
жинақтылығы шығады.
Даламбер белгісі. Егер  болып,
болып,  болса (1) қатар абсолют жинақты, ал
болса (1) қатар абсолют жинақты, ал  болса жинақсыз.
болса жинақсыз.
D облысында анықталған комплекс айнымалы функциялар тізбегінің мүшелерінен құралған мына өрнекті 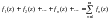 , (2)
, (2)
функционалдық қатар деп атайды.
Бұл қатар белгілі бір  нүктеде
нүктеде  сандық қатарына айналады. Егер
сандық қатарына айналады. Егер  сандық қатарыжинақты болса, онда (2)функционалдық қатар
сандық қатарыжинақты болса, онда (2)функционалдық қатар 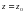 нүктеде жинақты деп атайды.Ал x0-ді функционалдық қатардың жинақтылық нүктесі дейді. Функционалдық қатаржинақты болатын нүктелердің жиынын қатардың жинақтылық облысы деп атайды.
нүктеде жинақты деп атайды.Ал x0-ді функционалдық қатардың жинақтылық нүктесі дейді. Функционалдық қатаржинақты болатын нүктелердің жиынын қатардың жинақтылық облысы деп атайды.

ақырлы қосындыны (2)-қатардың n-ші дербес қосындысы, ал D облысында анықталған
 функциясын (2)-қатардың қосындысы деп атайды.
функциясын (2)-қатардың қосындысы деп атайды.
D облысында  формуласымен анықталған
формуласымен анықталған  функциясы қатардың n –і қалдығы деп аталады. Егер
функциясы қатардың n –і қалдығы деп аталады. Егер  ұмтылғанда
ұмтылғанда 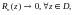 екендігі айқын.
екендігі айқын.
Функционалдық қатардың әрбір  нүктеде жинақталуын нүктеліжинақтылық деп атайды. (2)- қатар әрбір
нүктеде жинақталуын нүктеліжинақтылық деп атайды. (2)- қатар әрбір  нүктеде жинақты, және оның қосындысы
нүктеде жинақты, және оның қосындысы 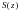 болсын.
болсын.
Қандай шарттар орындалғанда аналитикалық функциялардан тұратын жинақты қатардың қосындысы да аналитикалық функция болады?
А н ы қ т а м а(бірқалыпты жинақтылық).(2) функционалдық қатар D облысында 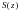 функциясына бірқалыпты жинақты деп аталады, егер кез келген
функциясына бірқалыпты жинақты деп аталады, егер кез келген  саны үшін
саны үшін 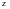 -тен тәуелсіз
-тен тәуелсіз  нөмірі табылып,
нөмірі табылып,  үшін және барлық
үшін және барлық  нөмірлері үшін
нөмірлері үшін
 теңсіздігі орындалса.
теңсіздігі орындалса.
Яғни,  , онда
, онда  ,
,  ,
,
1) Егер (2) қатар мүшелері D облысында үзіліссіз болып, қатар осы облыста бірқалыпты жинақты болса, онда оның қосындысы 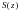 функциясы D облысында үзіліссіз болады.
функциясы D облысында үзіліссіз болады.
2) Егер (2) қатар мүшелері D облысында үзіліссіз болып, қатар осы облыста бірқалыпты жинақты болса, онда
 ,
,
мұндағы  - контурыD облысында жатқан кез-келген сызық.
- контурыD облысында жатқан кез-келген сызық.
3) Егер (2) қатар мүшелері D облысында аналитикалық болып, қатар осы облыста бірқалыпты жинақты болса, онда оның қосындысы 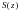 -те D облысында аналитикалық болады және
-те D облысында аналитикалық болады және
 ,
,
мұнымен қатар функциялар туындыларынан тұратын қатар да D облысында бірқалыпты жинақты.
18-теорема. (бірқалыпты жинақтылықтың Вейерштрасс белгісі). Егер  ,
, 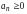 қатары жинақты болып, D- дан алынған кез келген z және
қатары жинақты болып, D- дан алынған кез келген z және  үшін
үшін  болса, онда (2) қатар D жиыныда абсолютті және бірқалыпты жинақты.
болса, онда (2) қатар D жиыныда абсолютті және бірқалыпты жинақты.
Кез келген мүшесі дәрежелік функция болатын қатарды дәрежелік қатар деп атайды.
 (3)
(3)
мұндағы 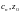 -комплекс сандар, ал
-комплекс сандар, ал  -комплекс айнымалы,
-комплекс айнымалы,  - дәрежелік қатардың коэффициенттері.
- дәрежелік қатардың коэффициенттері.
 болғанда
болғанда  (4)
(4)
қатарын аламыз.
Дәрежелік қатардың жинақтылық нүктелерінің жиынын қатардың жинақтылық облысы деп атайды.
Дәрежелік қатардың дербес қосындылары 
 -тен тәуелді функция болатындығы айқын. Сондықтан қатар қосындысы S те қатардың жинақталу облысында анықталған
-тен тәуелді функция болатындығы айқын. Сондықтан қатар қосындысы S те қатардың жинақталу облысында анықталған  -тен тәуелді функция болады:
-тен тәуелді функция болады: 
Дәрежелік қатарлар. Абель теоремасы. Жинақталу жиыны мен жинақталу радиусы.
Кез келген мүшесі дәрежелік функция болатын қатарды дәрежелік қатар деп атайды.
 (3)
(3)
мұндағы 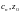 -комплекс сандар, ал
-комплекс сандар, ал  -комплекс айнымалы,
-комплекс айнымалы,  - дәрежелік қатардың коэффициенттері.
- дәрежелік қатардың коэффициенттері.
 болғанда
болғанда  (4)
(4)
қатарын аламыз.
Дәрежелік қатардың жинақтылық нүктелерінің жиынын қатардың жинақтылық облысы деп атайды.
Дәрежелік қатардың дербес қосындылары 
 -тен тәуелді функция болатындығы айқын. Сондықтан қатар қосындысы S те қатардың жинақталу облысында анықталған
-тен тәуелді функция болатындығы айқын. Сондықтан қатар қосындысы S те қатардың жинақталу облысында анықталған  -тен тәуелді функция болады:
-тен тәуелді функция болады:  .
.
19-теорема (Абель Нильс Хенрик (1802—1829) — норвегматематигі).
1) Егер (4) дәрежелік қатар  нүктеде жинақты болса, онда
нүктеде жинақты болса, онда  теңсіздігін қанағаттандыратын кез келген облыста ол қатар бірқалыпты және абсолют жинақты.
теңсіздігін қанағаттандыратын кез келген облыста ол қатар бірқалыпты және абсолют жинақты.
2) егер(4) дәрежелік қатар 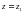 нүктеде жинақсыз болса, онда
нүктеде жинақсыз болса, онда  теңсіздігін қанағаттандыратын нүктелер жиынында ол қатаржинақсыз.
теңсіздігін қанағаттандыратын нүктелер жиынында ол қатаржинақсыз.
Абель теоремасы бойынша дәрежелік қатардың жинақтылық облысы дөңгелек болады.
Теріс емес R саны дәрежелік қатардың жинақтылық радиусы деп аталады.
Қатардың жинақтылық радиусын Даламбер және Коши белгілерін пайдаланып табуға болады.
1)  ; 2)
; 2)  .
.
Дәрежелік қатардың негізгі қасиетттеін атап өтейік.
1) (3) қатар жинақтылық дөңгінің ішкі нүктелерінде еабсолюттіжинақты, яғни  де.
де.
2) Дәрежелік қатар өзінің жинақтылық дөңгінің ішіндегі кез келген  дөңгелекте бірқалыпты және абсолют жинақты болады.
дөңгелекте бірқалыпты және абсолют жинақты болады.
3) Жинақтылық дөңгінің ішінде дәрежелік қатардың қосындысы 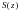 аналитикалық болады. 20-теорема. Егер
аналитикалық болады. 20-теорема. Егер  функциясы
функциясы 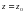 нүктенін, аймағында бірмәнді аналитикалық функция
нүктенін, аймағында бірмәнді аналитикалық функция
болса, онда ол осы нүктенің аймағында оң дәрежелер бойынша Тейлордың дәрежелік

қатарына жіктеледі. Бұлай жіктелгенде қатардың жинақтылық дөңгелегінің шеңбері  функцияның а нүктесіне ең жақын г айырықша нүктесінен өтеді, онын, центрі а нүктесінде болады.
функцияның а нүктесіне ең жақын г айырықша нүктесінен өтеді, онын, центрі а нүктесінде болады.
Жинақтылық радиусы былай өрнектеледі: 
 .
.
Тейлор қатарының коэффициенттері мына формулалар бойын-ша есептеліп шығарылады:


21-теорема. (жалғыздық теоремасы).  дөңгелегінде аналитикалық болатын кез келген
дөңгелегінде аналитикалық болатын кез келген  функциясы осы дөңгелекте Тейлор қатарына жалғыз әдіспен жіктеледі.
функциясы осы дөңгелекте Тейлор қатарына жалғыз әдіспен жіктеледі.
Е с к е р т у. 1. Кез келген дәрежелік қатар оның  қосындысының Тейлор қатары деп қарауға болады.
қосындысының Тейлор қатары деп қарауға болады.
2. Аналитикалық функциялар, тек солар ғана дәрежелік қатарға жіктеледі.
Олай болса, дәрежелік қатарлар арқылы аналитикалық функцияға мынадай анықтама беруге болады:
Егер  нүктесінің қандай да бір маңайында
нүктесінің қандай да бір маңайында  функциясы жинақты дәрежелік қатарға жіктетін болса, онда
функциясы жинақты дәрежелік қатарға жіктетін болса, онда  функциясын
функциясын  нүктесінде аналитикалық функция деп атайды.
нүктесінде аналитикалық функция деп атайды.
Дәрежелік қатардың қосындысының өз жинақталу дөңгелегінде голоморфты болатындығы туралы теорема.
Мына

Түріндегі қатарды комплекс облыстағы дәрежелік қатар деп атайды, мұндағы 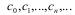
Коэффиценттері – мәні тұрақты комплекс сандар, z – тәуелсіз косплекс айнымалы.
(2.6) дәрежелік қатардың жинақты болатны барлық z мәндерінің жиыны осы қатардың жинақталу облысы деп аталады.
Абель теормасы: 1)Егер  нүктесінде (2.6) дәрежелік қатары жинақты болса, онда
нүктесінде (2.6) дәрежелік қатары жинақты болса, онда  теңсіздігін қанағаттандыратын кез келген z үшін берілген қатар абсолют жинақты болады.
теңсіздігін қанағаттандыратын кез келген z үшін берілген қатар абсолют жинақты болады.
2) Егер  нүктесінде (2.6) дәрежелік қатары жинақсыз болса, онда
нүктесінде (2.6) дәрежелік қатары жинақсыз болса, онда 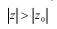 теңсіздігін қанағаттандыратын кез келген z үшін берілген қатар жинақсыз болады.
теңсіздігін қанағаттандыратын кез келген z үшін берілген қатар жинақсыз болады.
Анықтама:  шамасын (2.6) қатарының жинақталу радиусы деп, ал
шамасын (2.6) қатарының жинақталу радиусы деп, ал  дөңгелегін (2.6) қатарының жинақталу дөңгелегі деп атайды.
дөңгелегін (2.6) қатарының жинақталу дөңгелегі деп атайды.  дөңгелегін (2.6) қатарының жинақталады, ал осы дөңгелектің сыртында – жинақталмайды. (2.6) дәрежелік қатардың жинақталу радиусы мына формуламен анықталады:
дөңгелегін (2.6) қатарының жинақталады, ал осы дөңгелектің сыртында – жинақталмайды. (2.6) дәрежелік қатардың жинақталу радиусы мына формуламен анықталады:

Теорема. Кез келген дәрежелік қатардың суммасы
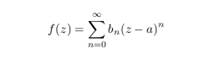
өз жинақталу дөңгелегінде голоморфты болады. F(z) үшін мүшелеп алынған дифференциалдық қатардың  туындысының дәрежелік қатарының қосындысы болып табылады.
туындысының дәрежелік қатарының қосындысы болып табылады.
Дәлелдеу: R арқылы f функциясының жинақтылық радиусын белгілейік және R>0 деп алайық. F(z) үшін мүшелеп алынған дифференциалдық қатарды қарастырайық:

Оның жинақтылық радиусы да R-ге тең, себебі  .
.
Бұл қатар мына теорма бойынша жинақтылығы анықталады. Дәрежелік қатар

Әрбір  үшін жинақталады, сонымен қоса
үшін жинақталады, сонымен қоса  компакті көпшілікте жинақтылық теңеседі. Осы теорема бойынша g теореманың2 шартынқанағаттандырады, яғни мыналарды:
компакті көпшілікте жинақтылық теңеседі. Осы теорема бойынша g теореманың2 шартынқанағаттандырады, яғни мыналарды:
1. G функциясы  үзіліссіз
үзіліссіз
2. Кез келген  үшбұрыш үшін
үшбұрыш үшін

Алғашқы функцияның бар болуы туралы теорема бойынша

интегралы U– да голоморфты жәнеU– да  шартын қанағаттандырады.
шартын қанағаттандырады.
G(ξ) үшін [a,z] бойынша мүшелеп интегралдау мынаған тең:

Бұдан f функциямыз U – да голоморфты және  дәлелдеуміз бойынша.
дәлелдеуміз бойынша.
Көрсеткіштік функция, оның қасиеттері. Эйлер формулалары. Тригонометриялык функциялар sinz, cosz, tgz, ctgz: барлық қасиеттері дерлік нақты жағдайдан көшіріледі. Бірақ,êsinzê>1 болуы мүмкін.
Комплекс облыстағы 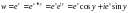 көрсеткіштік функция периодты. Оның периоды
көрсеткіштік функция периодты. Оның периоды  . Шынында да, кез келген бүтін n үшін
. Шынында да, кез келген бүтін n үшін  .
.
Тригонометриялық функциялар. Комплекс облыстағы  және
және  функциялары
функциялары
 ,
, 
формулалармен, ал 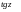 және
және  функциялары
функциялары
 и
и 
формулалармен анықталады.
Тригонометриялық функциялар үшін нақты айнымалының тригонометриялық функцияларының көптеген қасиеттері сақталады.  және
және  функцияларының периоды
функцияларының периоды  , ал
, ал 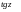 және
және  периоды
периоды 
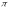 болады.
болады.
Нақты  нүктелері
нүктелері  функциясының нөлдері болатындықтан, осы нүктелерде
функциясының нөлдері болатындықтан, осы нүктелерде 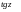 функциясы анықталмаған. Осы сияқты
функциясы анықталмаған. Осы сияқты  функциясының нөлдері болатын
функциясының нөлдері болатын  нүктелерінде
нүктелерінде  функциясы анықталмаған. Барлық тригонометриялық тепе-теңдіктер де сақталады. Бірақ комплекс облыстағы
функциясы анықталмаған. Барлық тригонометриялық тепе-теңдіктер де сақталады. Бірақ комплекс облыстағы  және
және  функциялары шенелмеген.
функциялары шенелмеген.
Гиперболалық функциялар келесі фрмулалармен өрнектеледі:

 ,
,  , яғни,
, яғни,  .
.
Дәрежелiк функция: голоморфтылығы, бірбеттілік еместігі, бірбеттілік облыстары.
Функция w=zn (1),
n- дәрежелік функция деп аталатын натурал сан.
Функцияның анықталу облысы барлық комплексті жазықтық болалады.
Егер n>1болса, онда дәрежелік функция өзара мәндес болмайды,яғни қайтымды бола алмайды. Егер  Муавр формуласы бойынша:
Муавр формуласы бойынша:


Осыдан шығатыны,  кезде (1)-ші теңдік орын алады егер
кезде (1)-ші теңдік орын алады егер
 бүтін болса.
бүтін болса.
w=z2кескінін толығырақ қарастырсақ. Осы кескіндеуде z аргументтері еселенеді,онда үстіңгі жарты жазықтық 
 UOV –ның барлық жазықтығында өтеді.
UOV –ның барлық жазықтығында өтеді.

Осы кезде ОА және ОВ сәулелері (3-суретте) UOV жазықтығына OU осьтің оң бағыты бойынша бір сәулеге өтеді. Өзара мәндес сәйкестіктермен жұмыс жасау ыңғайлы,яғни XOY жазықтығы бар ОА сәулесі осы қиманың O1A1 үстіңгі жағасына өтеді,ал ОВ – төменгі жағасына О1В1.
Дәл солай төменгі жартылай жазықтық 
 қиылған UOV жазықтығына өтеді,ОВ сәулесі үстіңгі жағаға,ал ОА- төменгіге өтеді. Кескіннің мәндестігін сақтау үшін, осы екі қиылған жазықтықты екі бөлек беттер деп санау оңай. Жағаларды жапсыру керек: ОА бірінші жазықтықтың үстіңгі жағасына және төменгі жаға екінші жазықтығынаөтеді. Дәл солай қиықтың бірінші жазықтығының төменгі жағасын қиықтың екінші жазықтығының төменгі жағасын жапсыру керек – осы екі жағалар бір ОВ сәулесінің кескіні болып табылады.
қиылған UOV жазықтығына өтеді,ОВ сәулесі үстіңгі жағаға,ал ОА- төменгіге өтеді. Кескіннің мәндестігін сақтау үшін, осы екі қиылған жазықтықты екі бөлек беттер деп санау оңай. Жағаларды жапсыру керек: ОА бірінші жазықтықтың үстіңгі жағасына және төменгі жаға екінші жазықтығынаөтеді. Дәл солай қиықтың бірінші жазықтығының төменгі жағасын қиықтың екінші жазықтығының төменгі жағасын жапсыру керек – осы екі жағалар бір ОВ сәулесінің кескіні болып табылады.
Алынған екібеттік бетті риман беті деп w=z2 функциясы үшін аталады.
Мысал1. АВС үшбұрышымен шектелген облыстың бейнесін табу керек.
А(-1;0); В(0;1), С(1;0) w=z2 кескіні кезінде.
Шешуі. w=z2=(x2-y2)+ixy.

 облыстың орғыту бағытын таңдаймыз(4-сур). А,В,С, нүктелерінің бейнесін және АВ,ВС,АС түзуін табамыз:
облыстың орғыту бағытын таңдаймыз(4-сур). А,В,С, нүктелерінің бейнесін және АВ,ВС,АС түзуін табамыз:
A=(-1;0) →A1=w(A)=1
B=(0;1) →B1=w(B)=-1
C=(1;0) →C1=w(C)=1.
AB: y=1+x. uжәнеvфункциялары үшін формуланы алмастырамыз:

Бірінші теңестіруден x табамыз және екінші теңестіруге қоямыз


Дәл солай ВС бейнесін аламыз: y=-x+1; ол парабола болады  СА түзуі: y=0 оң OU жарты жазықтығына өтеді.
СА түзуі: y=0 оң OU жарты жазықтығына өтеді.

ОС және ОА бір бейнеде болады,осы қиық бойынша оң жарты жазықтықты OU кесіп аламыз. Бейнелерді құрсақ А1,В1,С1. Облыстың орғыту бағытының сақталуы образдың өзінің бейнесін табуға рұқсат береді. (5-сур).
Комплекс сандар логарифмы. Логарифмдік функция. Комплекс санның комплекс дәрежесі.
Комплекс облыстағы логарифмдік функция көрсеткіштік функцияға кері функция ретінде анықталады, яғни, егер  болса, онда
болса, онда 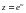 болады. Егер
болады. Егер 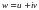 және
және 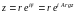 десек, онда
десек, онда  болады. Осылардан
болады. Осылардан  және
және  . Бірінші теңдңктен
. Бірінші теңдңктен  . Демек,
. Демек,
 .
.
Сонымен,  логарифмдік функция барлық
логарифмдік функция барлық  және
және  анықталған шексіз көп мәнге ие екендігін көреміз.
анықталған шексіз көп мәнге ие екендігін көреміз.  болғандағы мәні логарифмнің басты мәні деп аталып,
болғандағы мәні логарифмнің басты мәні деп аталып,  арқылы белгіленеді. Яғни,
арқылы белгіленеді. Яғни,  .
.
Нақты айнымалы комплекс мәнді функцияның кесінді бойынша интегралы. Сызықтық, аддитивтік, қасиеттері, айнымалыны алмастыру.
 z жазықтығында АВ үзік тегіс қисығы берілсін (А және В сәйкесінше қисықтың бастапқы және соңғы нүктелері).Осы қисықтың әрбір нүктесінде f(z) функциясы анықталсын деп ұйғарайық.АВ қисығын нүктелері
z жазықтығында АВ үзік тегіс қисығы берілсін (А және В сәйкесінше қисықтың бастапқы және соңғы нүктелері).Осы қисықтың әрбір нүктесінде f(z) функциясы анықталсын деп ұйғарайық.АВ қисығын нүктелері  болатын
болатын  доғаларына бөлейік.
доғаларына бөлейік.  арқылы
арқылы 
 ) доғаның ұзындығын белгілейік,
) доғаның ұзындығын белгілейік,  максимал ұзындық. Әрбір
максимал ұзындық. Әрбір  доғасында
доғасында  нүктесін алып интегралдық суммасын құрайық.
нүктесін алып интегралдық суммасын құрайық.


Егер  кезде интегралдық суммның соңғы шегі болса,онда бұл шекті
кезде интегралдық суммның соңғы шегі болса,онда бұл шекті  функциясының АВ қисығы бойынша алынған интегралы деп атайды және оны
функциясының АВ қисығы бойынша алынған интегралы деп атайды және оны  осылай белгілейді.Сонымен
осылай белгілейді.Сонымен
 АВ-интегралдау жолы.
АВ-интегралдау жолы.
(5.2) ескере отырып 
Соынмен комплекс айнымалы функцияның АВ қисығы бойынша алынған интегралы-екі нақты айнымалы комплекс мәнді қисық сызықты интегралдардың болуына парапар.
Сызықтылық
Егер  функциялары АВ үзік тегіс қисығында үзіліссіз болса,онда кез келген а және b тұрақтыларына
функциялары АВ үзік тегіс қисығында үзіліссіз болса,онда кез келген а және b тұрақтыларына  дұрыс.
дұрыс.
Аддивтивтілік АВ және ВС үзік тегіс қисықтары берілсін.Кез келген АС үзіліссіз қисығындағы  функциясына келес қатынас дұрыс:
функциясына келес қатынас дұрыс: 
Қисықтар, тегіс, үзік-тегіс қисықтар. Комплекс айнымалы функцияны қисық бойынша интегралын екі нақты екінші текті қисық сызықты интегралдар ретінде өрнектеу. Интегралдың қисық бағытына тәуелділік, біртектілік, доға бойынша аддитивтілік, функция бойынша аддитивтілік қасиеттері.
Жол деп  фукнциясындағы нақты t аргументінің және әрбір
фукнциясындағы нақты t аргументінің және әрбір  нүктесінде үзіліссіз болатын комплекс – мәнді функциясы.Кез келген
нүктесінде үзіліссіз болатын комплекс – мәнді функциясы.Кез келген 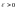 үшін
үшін  аймағы бар, ал t –ның барлық нүктелері үшін
аймағы бар, ал t –ның барлық нүктелері үшін  болады. a=z(a) және b = z(β) жолдың шегі деп атайды (егер α<β, онда а-басы, ал b аяғы болып есептеледі) Егер осы 2 нүкте тең болса, онда жол тұйық деп аталады. Мына 2 жолды:
болады. a=z(a) және b = z(β) жолдың шегі деп атайды (егер α<β, онда а-басы, ал b аяғы болып есептеледі) Егер осы 2 нүкте тең болса, онда жол тұйық деп аталады. Мына 2 жолды:  және
және  эквиваленті дейміз, егер
эквиваленті дейміз, егер  деген өспелі үзіліссіз функциясы барлық
деген өспелі үзіліссіз функциясы барлық  нүктелерінде
нүктелерінде  болса. Эквиваленттілікті екенін: рефлексифтілігінен
болса. Эквиваленттілікті екенін: рефлексифтілігінен  , симметриялығынан
, симметриялығынан
 және транзитивтылылығынан
және транзитивтылылығынан  білеміз. Енді, қисық деп жолдың эквиваленттілік класстарын айтады.Егер қисық жазықтыққа қатысты үздіксіз өзгерісте болса онда бұл қисық тегіс деп аталады. Ал, егер жазықтықтағы қисық тегіс доғалардың шекті сандарынан тұрса онда, оны үзік –тегіс қисықтар деп атайды.
білеміз. Енді, қисық деп жолдың эквиваленттілік класстарын айтады.Егер қисық жазықтыққа қатысты үздіксіз өзгерісте болса онда бұл қисық тегіс деп аталады. Ал, егер жазықтықтағы қисық тегіс доғалардың шекті сандарынан тұрса онда, оны үзік –тегіс қисықтар деп атайды.
Эквивалентті жолдардың класстарын ҚИСЫҚТАР деп атаймыз. Жол деп комплекс жазықтығында мынадай: үзіліссіз функцияны атайды. Жолдың комплекс түрде жазылуы:
Мынадай түрде берілген екі жолды эквивалент жолдар деп атаймыз.
Дата добавления: 2015-09-03; просмотров: 1018 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Комплекс айнымалының функциясы | | | Интеграл |