Лин. трансформатор при гармонич. воздействии. Вывод ур-й эл. равновесия в компл. форме. Экв. схема замещения трансформатора.

Лин. трансформатор – устр-во для передачи эн. из одной части эл. цепи в другую с использованием явления взаимоиндукции, представляет собой несколько связанных индуктивных катушек без общего ферромагнитного сердечника, эл. процессы в которых могут быть описаны лин. дифф. ур-ми.

Вывод ур-й эл. равновесия в компл. форме:

При гармонич. внеш. воздействии: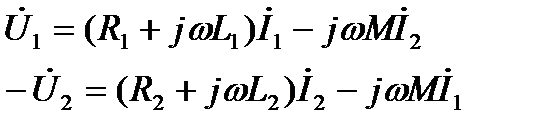

Используя экв. схему замещения без связанных индуктивностей:

Получаем следующие уравнения:

Экв. схема замещения лин. трансформатора:

-.

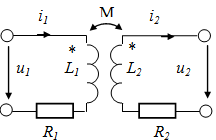
21. Приведенная к первичной обмотке эквивалентная схема линейного трансформатора при гармоническом воздействии. Идеальный трансформатор. Согласование комплексной нагрузки сопротивлением источника.

Идеальный трансформатор — трансформатор, у которого отсутствуют потери энергии на нагрев обмоток и потоки рассеяния обмоток. В идеальном трансформаторе все силовые линии проходят через все витки обеих обмоток, и поскольку изменяющееся магнитное поле порождает одну и ту же ЭДС в каждом витке, суммарная ЭДС, индуцируемая в обмотке, пропорциональна полному числу её витков. Такой трансформатор всю поступающую энергию из первичной цепи трансформирует в магнитное поле и, затем, в энергию вторичной цепи. В этом случае поступающая энергия равна преобразованной энергии:

P 1= I 1 U 1= P 2= I 2 U 2

где

P 1 - мгновенное значение поступающей на трансформатор мощности, поступающей из первичной цепи,

P 2 - мгновенное значение преобразованной трансформатором мощности, поступающей во вторичную цепь.

Соединив это уравнение с отношением напряжений на концах обмоток, получим уравнение идеального трансформатора:

U 2 U 1= N 2 N 1= I 1 I 2

Таким образом получаем, что при увеличении напряжения на концах вторичной

Согласование сопротивления нагрузки с генератором требуется для того, чтобы мощность, приходящая от генератора, полностью передавалась в нагрузку. При полном согласовании мощность распространяется только в направлении нагрузки, отраженная мощность отсутствует. Входной импеданс объемного резонатора в плоскости отверстия связи должен соответствовать волновому сопротивлению волновода или согласовываться с ним при помощи трансформирующего устройства. Сочленения и разветвления тракта также не должны вызывать отражений.

Согласование сопротивлений нагрузки с волновой характеристикой линии при помощи реактивных шунтов дает вполне удовлетворительные результаты в узкой полосе частот, составляющей 3 - 5 % от несущей или средней частоты. Такая полоса пропускания оказывается вполне удовлетворительной для всех видов передачи в одноканальных системах связи на средних и коротких волнах. На ультракоротких волнах при передаче телевидения или в многоканальных системах радиорелейной связи полоса частот расширяется до 15 - 20 % от несущей или средней частоты. Реактивные элементы, включаемые в линии для получения согласования сопротивлений, обычно обладают большой добротностью и имеют острую резонансную кривую.

Для согласования сопротивления нагрузки с выходным сопротивлением кристаллического триода обычно сопротивление нагрузки должно быть большим, а для согласования внутреннего сопротивления источника усиливаемого напряжения с входным сопротивлением триода внутреннее сопротивление источника должно быть малым. Такой подбор сопротивлений связан с большими трудностями, так как сопротивления нагрузок обычно малы, а внутренние сопротивления источников усиливаемых напряжений часто бывают велики; поэтому эта схема применяется редко. Она обычно непригодна для многокаскадного усилителя

22 Метод эквивалентного генератора.

.

Метод эквивалентного генератора, основанный на теореме об активном двухполюснике (называемой также теоремой Гельмгольца-Тевенена), позволяет достаточно просто определить ток в одной (представляющей интерес при анализе) ветви сложной линейной схемы, не находя токи в остальных ветвях. Применение данного метода особенно эффективно, когда требуется определить значения тока в некоторой ветви для различных значений сопротивления в этой ветви в то время, как в остальной схеме сопротивления, а также ЭДС и токи источников постоянны.

Теорема об активном двухполюснике формулируется следующим образом: если активную цепь, к которой присоединена некоторая ветвь, заменить источником с ЭДС, равной напряжению на зажимах разомкнутой ветви, и сопротивлением, равным входному сопротивлению активной цепи, то ток в этой ветви не изменится.

23 Осн. теоремы лин. цепей: обратимости, компенсации, об эквивалентном источнике.

Т. обратимости: Контурный ток k-го контура лин. пассивной цепи, вызванный действием ед. независимого источника напряжения, помещённого в i-й контур, равен контурному току i-го контура, вызванному действием того же источника напряжения, перенесённого из i-го контура в k-й (Если независимый источник тока, подключенный к какой-либо паре зажимов линейной пассивной цепи, вызывает на другой паре зажимов некоторое напряжение, то этот же источник тока, подключенный ко второй паре зажимов, вызовет на первой паре зажимов то же напряжение)

Доказательство: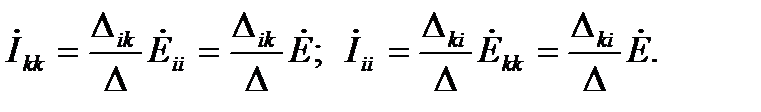

Учитывая симметричность матрицы контурных сопротивлений: D_ki=D_ik

Следовательно: I_kk=I_ii

Т. компенсации: Токи и напряжения произвольной эл. цепи не изменятся, если любую ветвь этой цепи заменить либо ид. источником напряжения, ЭДС которого равна напряжению данной ветви и направлена противоположно этому напряжению, либо ид. источником тока, ток которого равен току рассматриваемой ветви и совпадает с ним по направлению.

Доказательство:

Осн. система ур-й эл. равновесия каждой из цепей совпадает с осн. системой ур-й эл. равновесия исх. цепи. Замена Z_k ид. источником напряжения E_k соответствует переносу Z_kI_k из левой части ур-й баланса напряжений в правую со сменой знака. Ур-ия преобразованной цепи вместо тока I_k протекающего через Z_k содержат равный ему ток J_k ид. источника тока. Таким образом схемы являются эквивалентными.

Т. об экв. источнике: Ток любой ветви лин. эл. цепи не изменится, если автономный 2х-полюсник, к которому подключена данная ветвь, заменить экв. лин. источником энергии, который может быть представлен последовательной или параллельной схемой замещения. ЭДС ид. источника напряжения в послед. схеме замещения равна напряжению ХХ автономного 2х-полюсника, ток ид. источника тока в паралл. схеме замещения равен току КЗ автономного 2х-полюсника, а внутр. сопротивление и проводимость экв. источника равны соотв. компл. вх. сопротивлению и проводимости автономного 2х-полюсника.

АД – 2х-полюсник, напряжение ХХ или ток КЗ которого не равны нулю.

Компл. вх. сопр. 2х-полюсника – отношение компл. амплитуды напряжения на его зажимах к компл. амплитуде тока.

Доказательство:

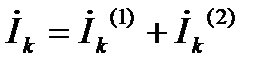
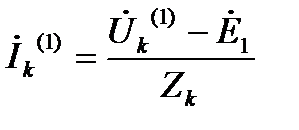
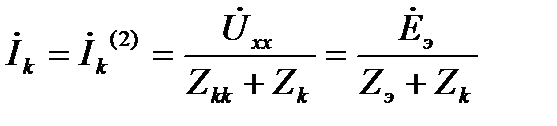
,где Z_э– компл. вх. сопр. исходного АД, равное компл. вх. сопр. НД.

Ток k-й ветви исх цепи равен току цепи, содержащей Z_k источник напряжения и компл. сопр. Z_э = Z_kk.

Ток ветви не изменился при замене АД экв. источником энергии, ЭДС которого равна напряжению ХХ АД, а внутр. сопротивление – его компл. вх. сопротивлению.

Дата добавления: 2015-08-21