Постулаты Г. Хакена и непоследовательность в динамике развития синергетики приводит к необходимости создания особого формального аппарата измерений биосистем 2 страница

Основываясь на этих трех предположениях (постулатах) можно измерять параметры квазиаттракторов – областей фазовых пространств, внутри которых происходит движение ВСБС. Причем, мы не отвергаем существование реальных аттракторов движения ВСОЧ, но они принципиально недостижимы для нас при измерениях. Постулируется некоторый аналог в измерении параметров этих реальных аттракторов с теоремой Бернулли (законом больших чисел), т.е., если число опытов (повторов измерений) производить неограниченно, то параметры квазиаттрактора (КА) будут приближаться к параметрам идеального аттрактора (как P*(A)→ P(A) при числе измерений n→∞). Но выше обозначенные 5 свойств БДС накладывают принципиальные ограничения на недостижимость измерений параметров идеального аттрактора, т.к. мы не можем удерживать сколь угодно долго БДС в приблизительно одинаковом состоянии (есть эволюция БДС, телеологически прописана смерть биосистемы, БДС постоянно кардинально меняется – человек болеет, стареет, меняет образ жизни и т.д.).

Поскольку число повторов n конечно и невелико, то приходиться довольствоваться параметрами квазиаттракторов. Алгоритм для их расчета содержит несколько действий, которые мы каждый раз выполняем при обработке данных, получаемых при измерениях x_i от группы биообъектов, находящихся приблизительно в одинаковом функциональном состоянии (условно одинаковое заболевание, одинаковые экологические условия, одинаковые физиотерапевтические воздействия и т.д.).

Кратко алгоритм расчета параметров квазиаттракторов ВСОЧ сводится к следующим действиям. Получаемые данные от группы пациентов или от одного пациента путем повторов измерений в виде набора блоков данных (компартментов), где -число измеряемых диагностических признаков, переносят в виде точек в -мерное фазовое пространство состояний ‒ ФПС. В этом ФПС фиксируя крайние левые и правые значения параметров вектора состояния организма человека по каждой координате ВСОЧ, образуют квазиаттрактор в виде m -мерного параллелепипеда, у которого определяется объем , центр квазиаттрактора и показатель асимметрии. По этим трём величинам (абсолютно или относительно) выносят решение об эффективности лечения, сравнивая эти параметры до воздействия (физкультурные упражнения, лечение) и после. При этом производятся измерения параметров функций организма каждого пациента из группы с одинаковой нозологической единицей или у одного пациента, но несколько раз (повторно) в приблизительно одинаковых условиях, в результате чего получают наборы данных по компонентам вектора состояния организма человека (т.е. по каждой координате ). Последние для каждого человека из группы (или для одного человека при одном измерении с повторами в дальнейшем) представляются в виде точки в -мерном фазовом пространстве состояний, где -количество диагностических признаков, используемых в диагностике при лечении (они же – компоненты ВСОЧ в ФПС) [81-93,178,179].

Таким образом, группа обследуемых больных образует некоторое “облако” в ФПС, которое имеет свои границы по каждой из координат (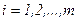). Эти границы образуют грани -мерного параллелепипеда в -мерном фазовом пространстве и каждая грань представляет уровень изменчивости (вариабельности) -го параметра (диагностического признака) – компонента вектора в ФПС. Общий объем этого параллелепипеда представляет объем некоторого квазиаттрактора , который для разных групп обследуемых (с разными нозологическими единицами, например) имеет свои параметры до и после воздействия (лечения, физической нагрузки, изменения возраста или места жительства). К этим параметрам относятся: объем квазиаттрактора , координаты центра квазиаттрактора в ФПС, показатель асимметрии , как расстояние между и центром средневзвешенного (координаты всех статистических математических ожиданий, т.е. среднего взвешенного).

Эти три параметра (, координаты центра квазиаттрактора и показатель асимметрии ) перед началом лечения (воздействия) имеют одни значения, а после лечения- другие. Разности между исходными и конечными этими интегративными параметрами, т.е. до начала лечения и после лечения (или на любом этапе после начала лечения, вплоть до его окончания), представляют количественную оценку степени эффективности проведения лечебного или лечебно-оздоровительного (профилактического, физкультурного) мероприятия. Эти величины могут быть абсолютными (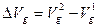, где после лечения ­­− и до лечения − ) или относительными, в процентах (). Если относительные изменения параметров квазиаттракторов превышают погрешность измерения диагностических признаков, то они уже считаются значимыми (во многих случаях это происходит от 5% или 10% и более). Чем больше изменения этих 3-х обобщенных (интегративных) показателей, тем более эффективно проводится лечебное или лечебно-оздоровительное мероприятие.

В рамках такого подхода автором и его коллегами сейчас строятся матрицы межаттракторных расстояний для разных групп больных (групп спортсменов, жителей разных территорий и т.д.). Определяются также параметры порядка (наиболее важные диагностические признаки), определяется степень синергизма в БДС и интервалы устойчивости биосистем (критерии устойчивости отличные от теории А.М. Ляпунова).

Уменьшение размеров квазиаттракторов ВСОЧ после различных воздействий (отдыха, лечения в санатории, физкультурных упражнений) свидетельствует о снижении уровня изменчивости (вариабельности), т.е. степени разброса параметров ВСОЧ в фазовом пространстве состояний для разных обследуемых групп людей. Отметим, что расширение границ квазиаттракторов сигнализирует о том, что некоторые обследуемые входят в область патологии, которая вполне еще и не проявляется. Однако измеряемые показатели ФСО уже сигнализируют о неудовлетворительной адаптации, отклонении от нормы. Очевидно, что после воздействий квазиаттрактор ВСОЧ часто сужается за счет нормализации всех функций отдельного организма или для всей группы обследованных людей с донозологическими формами. Если параметры ВСОЧ выходят за пределы 3-х сигм, то расширяются границы квазиаттракторов. Сейчас такой подход в измерениях используется нами как в медицине, так и в физиологии труда и спорта, экологии человека, в психофизиологии [26,61-93,156].

Известно, что важным свойством динамических систем с хаотической динамикой является свойство перемешивания. Свойство перемешивания более сильное свойство чем эргодичность и оно обеспечивает экспоненциальное убывание автокорреляционной функции (скорость этого убывания связана со скоростью сходимости меры к инвариантной). Существенно, что свойство перемешивания требует доказательств в каждом отдельном случае (если мы имеем адекватную динамическую модель реальной БДС). При этом, наличие положительного ляпуновского показателя (он характеризует экспоненциальное разбегание близких траекторий с течением времени t) не может гарантировать свойства перемешивания (т.е. хаотическую динамику БДС) и хотя имеются примеры именно это демонстрирующие (однако в общем нет доказательств и нет опровержения) или наоборот демонстрирующие, что скорость убывания автокорреляционной функции и скорость сходимости меры не связаны напрямую с ляпуновскими показателями, однако, на сегодняшний день общие подходы (теоремы), связывающие свойство перемешивания, динамики поведения автокорреляционной функции и ляпуновского показателя, автору не известны.

В целом, на сегодняшний день попытки измерять хаотичность в поведении различных динамических систем упираются в требование построения адекватной математической модели (а это уже исходно очень непростая задача для любой БДС, учитывая их 5 основных свойств), а затем возникает проблема изучения поведения БДС в пределах некоторых аттракторов, которая также в настоящее время не решена в общем виде (особенно проблема перемешивания). Все это подводит математиков и биологов уже к тому, что методы изучения поведения БДС в рамках хаоса на малых интервалах времени (меньших жизни биообъекта) носят спекулятивный характер (имеют характер допущений без строгих доказательств). Более того, существенно, что сами БДС в принципе не могут сколь угодно долго существовать в пределах фактического (биологически существующего временно) аттрактора. Эти аттракторы БДС смещаются, изменяют свои объемы и координаты центра (человек стареет, болеет, изменяет свое психическое или соматическое состояние) за довольно короткие интервалы времени (у человека за сутки и тем более за годы). Все это входит в пять основных свойств БДС, но не дает возможность их моделировать и не только в рамках ДСП, но и в рамках развивающейся синергетики (complexity).

Именно такие свойства аттракторов БДС (их нестабильность в фазовом пространстве и времени) приближает их к некоторому эквивалентному понятию в теории вероятности – ТВ, которое в ТВ характеризуется частотой , где - общее число испытаний. Практически, для всех БДС в ТВ и математической статистике (МС) мы пользуемся не вероятностью, а частотой (никто на практике n→∞ не устремляет, как того требует теорема Бернулли), а уже для 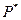находим приблизительные оценки функций распределений, их числовых характеристик и т.д. Иными словами в ТВ и МС частота события играет фундаментальную роль и на ней базируется все (гистограммы, математические ожидания, дисперсии и т.д. и т.пр.). Однако никто не говорит о том, что надо находить точное значение вероятности (например, путем n→∞) для БДС. Сейчас в ТХС (complexity) автор предложил ввести некоторое фундаментальное понятие для описания БДС, которое бы играло роль частоты в МС. Это понятие уже обозначено выше как квазиаттрактор. Оно не однозначное, но может сыграть роль базового понятия в ТХС и экспериментальной медицине и биологии. Действительно, вспомним роль частоты события в МС.

Традиционно считается, что для примерной оценки распределения вероятностей достаточно носитель меры (например, какую-либо область фазового пространства, содержащую носитель меры) разбить на достаточно малые подмножества и рассчитать достаточно длинную траекторию, содержащую точек . Тогда меру каждого такого множества можно оценить как , где - число точек, попавших в . Однако, если малы, а для БДС это обычное состояние из-за кратковременности их пребывания в относительно стабильном состоянии и невозможности контроля момента выхода из этого состояния, то возникает относительная погрешность и тогда приходится либо приближенно аппроксимировать меру гладким распределением, либо решать уравнение Перрона-Фробениуса, либо вообще отказываться от изучения таких систем (сейчас в биологии и медицине их просто грубо идеализируют).

Заметим, что уравнение Перрона-Фробениуса применимо для систем, у которых плотность вероятности не меняется под действием оператора (плотность вероятности инвариантная и ). Но этому условию удовлетворяют лишь отдельные модельные БДС, а реальные биосистемы имеют шумы. Тогда такие реальные БДС описываются не уравнениями 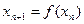, а уравнениями и при этом случайная величина распределена с плотностью , которая реально может непрерывно изменяться. В этом случае нельзя избавляться от сингулярных мер, а уравнения, подобные уравнению Хакена, не применимы. Более того, при переходе к физическим мерам очень часто вводят «специальные шумы», которые, например, не перебрасывают траектории БДС с одного аттрактора на другой (тогда задача упрощается и возможны какие-то решения) за счёт малой амплитуды шумов (обычно накладывают ограничения на дисперсию, что противоречит пятому свойству БДС, которое автор считает сейчас фундаментальным свойством любой БДС).

В действительности, все БДС не имеют шумы с малой максимальной амплитудой, для всех БДС характерно пребывание в некоторых аттракторах в течение суток или месяцев (хроноэкология) и тем более, если человек переходит от нормы к патологии, тогда аттракторы сразу изменяют свои параметры, а амплитуды вектора испытывает сильные возмущения.

При патологиях, особенно если они повторяются многократно (например, при хронических заболеваниях, заболеваниях периодического характера (малярия)) и тем более, если учитывать старение и смерть организма (старение требует возрастной смены аттракторов), мы будем получать и большие амплитуды и частую смену аттракторов. Более того, базовым свойством БДС является их постоянная возможность выхода за пределы 3-х сигм (а это в принципе дает очень большие амплитуды в фазовых пространствах состояний). Это можно трактовать как сильную вариабельность параметров реальной БДС, которая якобы находится в стационарном состоянии (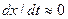), но реально движется в пределах некоторого аттрактора (автор его обозначает как квазиаттрактор в ФПС).

Таким образом, многие требования, которые накладываются на БДС для их возможного описания в рамках теории динамических систем (и уж тем более в рамках ТВ и МС) не позволяют их описывать уже разработанными и апробированными математическими методами (N_i малы, аппроксимация Фробениуса невозможна). Однако, возможен еще один подход, который базируется на гипотезе о том, что в ТХС существует некоторый аналог теоремы Бернулли для описания динамики поведения систем с хаотической динамикой. Можно предположить, что вектор состояния БДС движется в пределах некоторого аттрактора (будем называть его квазиаттрактор) и параметры такого квазиаттрактора (его объем в ФПС, координаты центра и др.) представляют истинный (идеальный) аттрактор аналогично тому, как частота события (мера каждого множества m(A_i)= N_i/N, см. выше) описывается его вероятностью P(A). Априори понятно, что БДС – это мерцающие и эволюционирующие системы и для них определять параметры аттракторов в принципе невозможно (нельзя N→∞, нельзя БДС наблюдать сколь угодно долго, т.к. они постоянно меняются). Тогда некоторый экспериментальный срез (на участке некоторого времени τ при N сравнительно небольших), который будет представляться равномерным распределением (вместо неравномерного распределения плотности вероятности H(х)), будет приближенно представлять квазиаттрактор и для такого квазиаттрактора можно рассчитывать некоторые аналоги частоты P*(A), что делается в математической статистике в МС. Фактически, такое предположение эквивалентно гипотезе, что на малых τ и при малых выборках N любая БДС имеет хаотическую динамику поведения, и эта динамика укладывается в пределах некоторого квазиаттрактора в ФПС (за счет самоорганизации, телеологичности, существования реальных (или гипотетических) внешних управляющих воздействий – ВУВов).

Поскольку подтвердить или опровергнуть эту гипотезу на сегодняшний день не представляется возможным для любых природных БДС, а другие методы просто использовать нельзя (шумы по амплитуде велики, N_i малы и т.д., см. выше), то в рамках этой гипотезы мы попробовали выполнить расчеты параметров квазиаттракторов для разных состояний организма человека или животных, находящихся в состоянии нормы или патологии, в условиях физических нагрузок (да еще и разных видов) и без таковых, в условиях действия некоторых экологических факторов и без таких воздействий. В общем, диапазон объектов, которые мы рассмотрели, огромен как по количеству, так и по качеству (огромное разнообразие объектов и их состояний). Алгоритм расчётов параметров квазиаттракторов представлен выше в этой главе, а вот результаты таких расчётов изложены в 32 монографиях и почти 400-х статьях [26,60-93,162-164,178,179,227-235,237].

При этом оказалось, что во всех исследуемых случаях были получены существенные различия по значениям параметров квазиаттракторов. Было установлено, что их объёмы (V_g) и координаты их центров смещаются (изменяются) весьма закономерно и устойчиво. Каждая патология имеет свои параметры. Более того, увеличивая N, мы могли использовать и статистические методы измерения параметров квазиаттракторов (задавая объемы по среднеквадратическим отклонениям или доверительным интервалам, а координаты центров стохастических квазиаттракторов определялись по статистическим математическим ожиданиям). Динамика изменения параметров квазиаттракторов в гипотезе равномерного распределения и в гипотезе неравномерного распределения оказалась, в основном, несколько сходной, но наблюдались и существенные численные различия.

В целом, нами был установлен ряд явлений. Например, оказалось, что при переходе из одного квазиаттрактора в другой (от нормы к патологии или наоборот) практически все объемы квазиаттракторов давали некоторое увеличение (при патологии) или уменьшение (при переходе к саногенезу). Таким образом, можно говорить о том, что БДС при смене режимов (или внутренней перестройки) увеличивают свою вариабельность (говоря физическим языком, флуктуации нарастают) или уменьшают вариабельность (при нормогенезе). Такой процесс может характеризовать систему, как переходящую в другие режимы (или выход за пределы квазиаттрактора и начало катастрофических процессов в динамике поведения БДС). Более того, уменьшение размеров и положения квазиаттракторов в ФПС очень выражено характеризуют процессы старения организма и попадания в мортальный аттрактор (приближая организм к смерти). Динамика параметров квазиаттракторов показывает существенные различия между биологическим и физическим возрастом, условиями жизни на Севере РФ, демонстрирует различия в реакциях ФСО на различные виды физических нагрузок (виды спорта), на разные патологии, возрастные различия и т.д.

Фактически, такая постановка проблемы сводится к 2-м подходам в изучении БДС: подход И. Пригожина (основан на познании сложности, термодинамике неравновесных систем и нелинейной динамики в целом) и подход Г. Хакена (переходы «хаос-порядок», системный синтез, синергетика как противоположность кибернетики из-за наличия положительных связей между подсистемами, телеологичность….). Сейчас эти два подхода (в США это complexity по И. Пригожину, а в Германии – синергетика по Г. Хакену) пытаются противопоставить, и дело доходит до антагонистических дискуссий, но эти все противоречия – кажущиеся. В этих двух подходах исследуются одни и те же (человекомерные по С.П. Курдюмову) системы, которые обладают уникальными свойствами. Но что действительно имеет принципиальные различия, так это физико- химические системы и человекомерные системы. Между ними пропасть и поэтому попытки описывать БДС в рамках ДСП ‒ это иллюзия и наоборот подтягивать БДС под модели ДСП ‒ это выдавать желаемое за действительное.

Главное в этих различиях это: 5 свойств БДС (которые были указаны в этой главе), постулат Г. Хакена о бессмысленности работы с одним элементом системы (важен компартмент или кластер и это уже проявляется на уровне воды - работы Е.П. Хижняка [179]) и постулат автора этой книги: одна точка в ФПС даже для компартмента (или кластера) не имеет существенной информации. Последнее свойство (критерий) самое существенное, т.к. до настоящего времени все модели БДС (и любых человекомерных систем) были выполнены в рамках ДСП, а это означает, что dx/dt=0 (или const) возможно и такие системы можно описывать точками и линиями в ФПС.

Сейчас автор постулирует, что это не соответствует действительности (dx/dt≠0 или dx/dt≠const), а любая БДС даже в покое находится в квазиаттракторе ФПС и параметры этого квазиаттрактора являются важной характеристикой состояния любой человекомерной системы (и БДС, в частности). Это значит, что хаос БДС имеет место не только на макроуровне, но и на микроуровне (для БДС, находящихся якобы в стационарных состояниях). Это значит, что надо наблюдать не линии и точки, движущиеся в ФПС, а “облака” (объёмы квазиаттракторов) и параметры этих облаков характеризуют состояние человекомерных систем. Таковы новые реалии природы и с этим необходимо считаться.

Шесть фундаментальных вопросов человечества к синергетике и ответы на них в рамках третьей парадигмы

Как известно, в мире сейчас существует несколько центров, которые пытаются изучать сложные системы, способные к самоорганизации, эволюции, но находящиеся в постоянном динамическом взаимодействии с другими объектами, с окружающей средой в целом. Отметим, что этих объектов в природе великое множество (начиная от клетки, человека и кончая Вселенной), а значит речь идет о познании всего сущего, но с несколько других позиций. Об этих позициях автор уже говорил многократно и достаточно подробно, поэтому достаточно напомнить, что речь идет о трансформации системы познания в целом, о переходе от детерминистского подхода к стохастическому (в целом, это детерминистско-стохастический подход – ДСП), а от него к новой синергетической парадигме, к теории и синергетике.

Сейчас легко назвать несколько центров по изучению сложности (синергетики) в США (это легендарный институт Санта – Фе (SFI) во главе с Мюррей Гелл-Маманиом и Джорджем Коуэном, группа нелинейной динамики в Калифорнии), в Германии (группа по изучению наследия и развития идей Л. Фон Берталанфи, Институт междисциплинарной информатики, Университет Лугсбурга во главе с нынешним лидером Клаусом Майнцером – профессором кафедры философии и теории науки и почетным руководителем этой группы – Германом Хакеным), имеются аналогичные объединения ученых в Италии, Франции и других странах. Однако они отсутствуют в России, хотя (по справедливому замечанию Д.С. Чернавского и ныне покойного В.С. Курдюмова [112]) именно Россия исторически и традиционно развивала и поддерживала целые научные школы (Д.И. Менделеева, В.И. Вернадского и др.), которые имели междисциплинарный подход в своей деятельности. В чем причина отставания в развитии междисциплинарных подходов в современной РФ?

Прежде всего дело тут не в отрицании западных методов (в СССР) или наоборот, преклонении перед ними в нынешней, капиталистической России, как отмечает Д.С. Чернавский. И даже не в том, что вся наука РФ финансируется по остаточному принципу («на тебе боже, что нам негоже»), хотя это имеет место уже 20 лет (бюджет университета Калифорнии в 2000 г. превосходил бюджет РФ на всю науку!) и потери РФ в качестве и количестве интеллектуальной элиты будут не восполнимы ближайшие 50 лет (а падали то всего 20 лет).

Общество и его властная верхушка – Государство российское не хочет понимать одну простую вещь отсутствие финансирования науки (именно отсутствия, а не недофинансирования) закрывает нам дорогу в знаниевое, информационное, постиндустриальное общество (ЗСПО). Именно закрывает, т.к. создание и передача знаний процесс каталитический: поддержка интеллекта, как цепная реакция нарастает качество и количество интеллектуальной элиты в РФ, а отсутствие поддержки – по типу цепной реакции ухудшает качество и количество интеллектуальной элиты. Иными словами: знания порождают знания и прогресс, а незнания порождают незнания и регресс. Это хорошо видно на деградации РАН, которая за 20 лет быстро превратилась из собрания ученых в собрание людей, которые могут попадать в РАН не по своим научным заслугам (книги, статьи, открытия и вновь попадающих находятся в меньшинстве) а по своим финансовым, административным и политическим возможностям. Более того, у меня деловое предложение Правительству РФ переименовать РАН в МАН (московскую академию), т.к. около 80% членов РАН – это жители Москвы и её окрестностей, а других членов МАН числить как почетными иногородними членами. Против финансирования по остаточному принципу, против трансформации РАН в МАН, против разрушения НИИ и интеллектуальной элиты РФ в целом; уже начались стихийные протесты. О них говорят также стихийно, спорадически, без системы: уехало более 200 тыс. учёных из РФ (президент приветствует их отъезд из РФ, «летите, голуби, летите», учёный Перельман отказался от премии (подчеркивая тем самым, что учёный в РФ может жить (и живет) без денег и без работы в НИИ – этакий учёный-домушник (почти как вор-домушник), а это ведь на Руси называлось юродствованием (в хорошем смысле!), ученики после школы не идут в вузы на естественные и точные науки (конкурсов нет, а то, что приходит – «на тебе боже, что нам негоже»), конкурсы пропали даже в Москве. Но самое главное, кто на наше место придёт, кто через 20-30 лет будет профессорами, учёными в вузах и НИИ? Где смена, господа? Из США и Англии организуете возврат 200 тыс. уехавших? За 650 часов нагрузки в РФ мы имеем в 24 раза меньшую заработную плату, чем бельведерский профессор в Польше!).

Да и кто поедет в страну, где Президент говорит: «…в науку вкладывают средства чудаки». Видимо к этим чудакам государство себя никак относить не хочет, а других «чудаков» в России мы тем более не найдем. Нет у нас и людей (по рангу в РАН или по экономической независимости в стране) подобных Гелл-Манну, и даже нет подобных академику А.И. Бергу (по интеллекту, по степени влияния на Правительство РФ), которые бы смогли переломить ситуацию, которые бы могли издать Совет или запустить государственную программу по поддержке и развитию 3-й парадигмы (после ДСП) в России (как это было с кибернетикой, когда был издан Совет по кибернетике и ряд институтов). Нет понимания и доброй воли у членов правительства РФ, т.к. отсутствие интеллекта порождает (автоматически) дальнейшее отсутствие интеллекта.

Знание порождает знание, а незнание порождает иллюзию знания (более глубокое незнание на самом деле). Человек получает власть (становиться президентом, премьером, президентом РАН) и ему уже кажется, что он всё знает, всё умеет, рождается иллюзия правильного принятия решений, но на самом деле все эти люди создают оптимальную систему удержания связей, личной власти. Это достигается любой ценой и поэтому сейчас менделеевы и вернадские не в почете. Их знания и научный опыт никому не нужны в России. По этой причине у нас никогда (!) не возникнут аналоги SFI, т.к. такие институты не нужны бизнесменам (дураки вкладывают в науку!), не нужны потомкам (они не поддерживают временщиков – правителей, существующие режимы) и они не решают сиюминутные задачи общества (не кормят голодных, не учат безграмотных, не …)

Дата добавления: 2015-10-23