Постулаты Г. Хакена и непоследовательность в динамике развития синергетики приводит к необходимости создания особого формального аппарата измерений биосистем 1 страница

При изучении основных свойств систем, претендующих на объекты синергетики, в настоящее время существует два подхода, которые принципиально разделили синергетику на несколько кластеров знаний (якобы раздельных наук). В рамках первого подхода, который активно развивал И.Р. Пригожин и который запомнился образованием ряда новых направлений (сейчас они признаны в США как complexity nonlinear dynamics - NLD и теория неравновесных систем - ТНС) лежат представления о сложных системах, которые обладают высокой степенью неопределенности, но которые можно описывать в рамках давно существующих детерминистской и стохастической парадигм (ДСП). Такие объекты, процессы и явления могут описываться некоторыми уравнениями (дифференциальными, разностными, в частных производных или интегро-дифференциальными уравнениями), в которых неопределенность поведения изучаемых, якобы синергетических, объектов появляется из-за особых свойств этих самых уравнений.

В целом, такой подход (его создал и активно развивал И.Р. Пригожин) имеет в основе классические детерминистскую и стохастическую парадигмы. Что характерно для ДСП? Во-первых, все объекты, изучаемые в ДСП, должны иметь всегда исходные состояния вполне определенные, повторяемые (воспроизводимые), а дальнейшее развитие изучаемого процесса должно быть предсказуемым и определенным (в рамках детерминистской парадигмы или прогнозируемым в виде известных исходов в рамках стохастической парадигмы). В последнем случае вариантов исхода может быть ограниченное количество или бесконечное, но они как-то все-таки повторяются. Эти исходы представляются в виде набора возможных состояний и при этом главное, что эти состояния могут быть проверены. О чём идет речь?

Всегда в теории вероятности или математической статистике любой экспериментатор может воссоздать исходные состояния и повторить динамику протекания процесса, после чего мы получим результат опыта (или наблюдения) и эти результаты после многократного повторения обеспечат расчёт частоты события, которая по теореме Бернулли в конечном итоге будет представлять вероятность события. Именно в повторении, воспроизведении любого процесса в точности (если процесс детерминистский, то такое бывает только в идеале) или в пределах каких-то значений (если процесс стохастический). Однако в последнем случае конечные состояния системы все-таки прогнозируются в рамках каких-то значений [239-248,255-266,272-276,294].

Существенно, что вполне определённые или неопределённые, прогнозируемые с какой-либо частотой (или вероятностью) процессы (состояния системы) образуют огромные кластеры объектов, которые изучаются в физике, химии, технике. И они могут описываться некоторыми уравнениями (точно или с вероятностью). Проблема И.Р. Пригожина и его последователей заключается в том, что используя неопределенность таких систем (например, термодинамических систем, где число состояний огромно, т.к. такие системы состоят из огромного числа элементов), была попытка перебросить мостик в изучение совершенно других систем: биологических, медицинских, социальных и других [255-268,272-284,286-293].

Действительно, термодинамические системы во многом сходны с социальными и медико-биологическими системами. Это сходство основано на множественности (огромном числе элементов, связей между ними, огромном числе промежуточных состояний и особенно огромном числе конечных состояний). Их изучение сейчас в США идет под флагом complexity, nonlinear dynamics, термодинамических неравновесных систем и даже теории хаоса (chaos). Но все такие системы (с изучения которых начинал И.Р. Пригожин) обладают одним существенным общим свойством (характерным для физических, химических или технических систем) – они исходно воспроизводимы и они повторяемы. Любую термодинамическую систему можно воссоздать и воспроизвести ее состояние в любой момент времени (хотя бы в рамках каких- либо функций распределений) [191-198,215-225,237-340].

Иные объекты стал изучать и моделировать Г. Хакен в новой науке, которую он назвал синергетикой. Он начал изучать объекты, которые в принципе нельзя повторить в пространстве и времени. Г. Хакен впервые обратил внимание ученых на существование таких объектов. К ним относятся: человек и его биосистемы (например, функциональные системы организма (ФСО)), животный мир и биосфера Земли в целом, сама Земля и все космические объекты, которые единичны и случайны, а их динамика не воспроизводима и неповторима. Нам нельзя повторить (второй раз) эволюцию человека, Земли, Вселенной. Все такие системы С.П. Курдюмов стал называть человекомерными системами, и они не повторяемы и не воспроизводимы в принципе [105-107].

Г. Хакен это понимал, но пойти дальше в их изучении не смог. В его постулатах по синергетическим объектам (табл. 1.1 стр. 16 [181]) зафиксирована только одна сторона этих объектов (с которой, кстати, соглашался и И.Р. Пригожин) – эти объекты сложные, число элементов их составляющих, огромное и их невозможно оценивать по отдельности. Отсюда вывод – синергетика не работает с отдельными элементами, ее объекты – сложные системы, где единица – ничто, а важна коллективная динамика (отсюда и внимание процессу самоорганизации). Однако в коллективном взаимодействии не обязательно будет самоорганизация (в термодинамических системах И.Р. Пригожина ее нет), да и сам термин самоорганизация довольно неопределенный, он формально (математически) не идентифицируется.

Таким образом, в представлениях Г. Хакена в объектах, которые изучает синергетика, важна непредсказуемость, которая возможно ликвидируется за счет самоорганизации.

Но детального изучения неопределенности Г. Хакен не выполнил. Он ограничил свою неопределенность рядом сложных характеристик: неопределенность в числе элементов, образующих сложную систему (complexity), неопределенность в характере и законах всех взаимодействий между элементами таких сложных систем, неопределенность в динамике развития процесса и его конечного состояния. Все эти неопределенности есть и у И.Р. Пригожина, в работах его последователей. Такая неопределенность есть во всех термодинамических системах (они содержат много элементов и невозможно описать законы их взаимодействия).

Однако имеются более значимые неопределенности особых синергетических объектов, о которых не говорил И.Р. Пригожин и обошел их обсуждение Г. Хакен. Речь идет о неопределенностях в различных состояниях синергетических объектов: в начальном состоянии х₀=(t) изучаемой системы, промежуточных состояниях x_i=(t) и, наконец, конечном состоянии х_к=(t) сложных биологических или социальных систем. Существенно, что эту проблему автор уже обсуждал (см. табл. 1.1) и ещё будет обсуждать на страницах настоящего издания неоднократно (в разных аспектах), т.к. эта проблема имеет важнейшее значение для становления и развития синергетики как науки и как третьей парадигмы. При этом речь сейчас пойдет не о таблице 1.1 (см. гл.1), которая включает в себя три подхода (детерминизм – det., стохастику - stoch., и, синергетику (или хаос) – synerg.), а более детальное рассмотрение самых базовых понятий: синергетика и теория хаоса.

Действительно, если в обычных авторских таблицах 3*3, где в 1-ой строке перечисляются состояния изучаемых объектов (систем) т.е., х₀=(t) – начальное, x_i=(t) - промежуточные состояния, х_к=(t) - конечное состояние, а по вертикали откладываются определения (названия) трех парадигм, в рамках которых изучаются эти состояния (т.е. det., stoch., synerg.), то теперь автор вынужден более детально поговорить о самой третьей парадигме, которую он часто обозначал, как теория хаоса и синергетика (ТХС). Почему именно ТХС? Это объясняется не только тем, что процессы самоорганизации (возникновения порядка из хаоса как первоначально обозначали синергетику) лежат в основе, синергетики, но и тем, что понятие хаоса автор рассматривает в более широких пределах, которые превосходят традиционное понимание этого особого состояния – хаос. С чем это связано?

Сейчас уже можно говорить о микрохаосе, когда БДС не находится в стационарном состоянии (dx/dt≠0, x≠const) и параметры её все постоянно варьируют и вектор находится микрохаотическом режиме. Тогда в табл.1.1 (глава) третья строка в отношениях к представлениям И.Р. Пригожина и его последователям (моделируемый хаос, когда 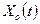задан определённо). У нас же, если следовать представлениям Г. Хакена и убеждению автора этой книги, начальное состояние системы (человекомерной, БДС) никогда определённым не будет (именно задать только квазиаттрактор) и появляется четвёртая строка, в которой мы имеем все минусы (на микроуровне все не определены). В этом случае мы работаем только с квазиаттракторами. А модели можно использовать только для квазиаттракторов, внутри которых ВСС имеет равномерное распределение (если нет главных законов управления на БДС и система находится в микрохаосе). Тогда таблица 1.1 из (главы 1) переходит в таблицу 5.1 и все модели из ДСП теряют смысл. Точнее говоря их можно использовать, но условно, и лучше для уже совершённых процессов (как модели прошлого), т.к. будущее в ТХС не прогнозируется, а есть только аттрактор, куда БДС попадает под действием ВУВов.

Таблица 5.1

	Начальное состояние	Промежуточное состояние	Конечное состояние
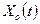
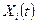
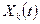
Deterministic	+	+	+
Stochastic	+	±	–
Chaos (И. Пригожин)	±	–	–
Chaos (Г. Хакен и автор)	–	–	–

Для понимания этого тезиса напомним, что в традиционном определении хаотического состояния объекта всегда существовало 2 подхода (или 2 определения). Во-вторых, для хаоса характерно такое состояние системы, когда определение начального состояния (задание вектора состояния системы в точке t=0, т.е. х₀=(t)) системы не определяет ее дальнейшую траекторию (т.е. x_i=(t)) и (или) конечное состояние системы (т.е. х_к=(t)). Это первое определение хаоса имеет скорее динамический характер, т.е. основывается на поведении системы и не определяет состояние хаоса любой биологической динамической системы (т.к. не обеспечивает идентификацию хаоса динамической системы по ее моментальному “снимку”, т.е. по анализу мгновенного состояния изучаемого объекта). Такой хаос автор признаёт на макроуровне и только как идеал, как гипотетическую модель, т.к. БДС постоянно варьируют.

Имеется второй метод определения хаотического состояния системы, если она находится в некоторых динамических режимах, характеризующихся наличием бифуркаций рождения циклов. В этом случае, если система имеет уже колебательный режим работы, имеется некоторая частота колебаний 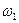и затем на фоне колебаний с 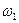возникают бифуркации рождения циклов с другими частотами 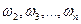. При n→∞ (т.е. число колебаний, гармоник начинают резко увеличиваться до бесконечности), мы можем тоже говорить о переходе системы в хаотический режим. Это определение хаоса тоже весьма эффективно, но оно, как и предыдущее, имеет динамический характер, т.е. надо наблюдать систему длительное время, в динамике ее развития. Этот метод тоже не является одномоментным (по мгновенному снимку изучаемого процесса мы не можем сказать о хаотическом режиме поведения вектора состояния системы - ВСС). Таких два динамических метода идентификации хаоса в БДС (или других complexity) требуют длительного наблюдения динамики поведения ВСС в фазовом пространстве состояний и построения адекватных моделей. А это очень сложное дело.

Существует еще ряд подобных динамических методов определения хаотических режимов, например, метод анализа скорости убывания автокорреляционных функций, или метод оценки ляпуновских показателей (характеризуют экспоненциальное разбегание близких траекторий в фазовом пространстве состояний с течением времени). Но все эти методы (и им подобные) относятся уже к методам с моделированием, т.е. необходимо сначала подобрать (построить) некоторую модель процесса. При этом сразу возникает вопрос: на сколько она адекватна этому процессу, т.е. валидна ли она, а такие проверки – это целая область знаний, и они не имеют универсальных методов, т.е. имеется сугубо индивидуальные особенности для каждого процесса и для каждой модели.

В целом, можно отметить, что первые определения (и модели на их основе) хаотических режимов функционирования сложных систем (complexity) сложны из-за необходимости наблюдения ВСС (возможно очень длительно). Вторые методы требуют создания адекватных моделей поведения ВСС и сразу возникают вопросы их проверки, да и точности идентификации самих режимов (на предмет их хаотичности). Вместе с тем, кроме этих (весьма сомнительных, по мнению автора, и он ниже скажет, почему) динамических методов существует некоторый универсальный метод, который приближается к разовому снимку процесса. Это метод, основанный на свойствах перемешивания. Такой метод на сегодняшний день является самым универсальным, самым точным и самым доступным. Этот метод и следует развивать в синергетике, но автор предлагает некоторые модификации этого метода для целей медико-биологических систем и других сложных систем.

Рассмотрим более подробно всю эту проблему в комплексе, т.е. не только в определении хаотических режимов, идентификации хаоса как такового, но и в самих методах определения хаоса, в вопросах устойчивости хаотических режимов, поскольку обычно в математике особое внимание всегда уделялось вопросам устойчивости стационарных режимов (т.е. когда x(t)=const) или вопросам устойчивости колебательных режимов (бифуркациям рождения циклов). А вот вопросам устойчивости хаотических режимов особого внимания в науке вообще не уделяется. В синергетике считается, что биосистемы с самоорганизацией долго в хаосе пребывать не могут, они обязательно должны переходить в другие режимы, но если усомниться в этой догме, то открывается другое мировоззрение и другие перспективы изучения БДС и других человекомерных систем (по С.П. Курдюмову).

В рамках этого нового подхода делается новое (и второе, дополненное к гипотезе Г. Хакена) предположение: в синергетике не только не имеет смысла работать с отдельным элементом в ФПС (см. табл.1.1. стр. 16 [181] в виде постулата Г. Хакена), но не имеет смысла работать и с одним состоянием одного (или многих элементов) элемента системы. Иными словами одномоментное состояние одного элемента (или их совокупности) в данный момент времени не имеет никакого значения. Для оценки динамики поведения можно наблюдать и один элемент (изучать ФСО одного человека), но делать это надо достаточно долго и приблизительно в одинаковых условиях.

Исходя из этого постулата мы будем говорить, что “единица – ничто и единица – всё”. Именно такой тезис принят в синергетике сообществ (см. ниже схему в главе 7). Это базовый принцип организации синергетических систем не только социальных, но и любых других. В рамках этого принципа сейчас мы говорим, что одна точка (состояние одного элемента системы) в ФПС не имеет особого значения, но совокупность таких точек образует облако, а параметры этого облака (точнее квазиаттрактора, внутри которого находится это облако) весьма информативны для описания поведения и прогноза любых человекомерных систем (БДС, социальных, политических, педагогических и т.д.). Для более реального осознания степени неопределённости в изучении самого хаоса остановимся весьма кратко на формальном аппарате для измерения биосистем, как наиболее характерных и массовых представителей человекомерных систем.

В этой связи, прежде всего, отметим, что в настоящее время в клинической кибернетике происходит осознание того, что организм человека, как сложная биологическая динамическая система (БДС), является объектом новой науки синергетики (или complexity, как её называют в США). Такие сложные БДС имеют 5 характерных свойств (признаков), которые показывают неправомерность применения методов детерминистского или стохастического подхода в описании подобных (человекомерных систем по С.П. Курдюмову) систем. Эти пять свойств делают объекты, изучаемые в рамках синергетики, совершенно отличными от объектов физики, химии, техники, которые могут описываться в рамках ДСП.

Не останавливаясь подробно на всех особенностях «человекомерных систем» (по С.П. Курдюмову) и в частности «биосистем», о которых автор уже неоднократно писал в разных публикациях, хотелось бы кратко отметить именно пять базовых свойств биологических динамических систем (БДС), понимание которых имеет принципиальное значение для разработки новых концепций при их (БДС) изучении и построении моделей их поведения в рамках СП. Эти свойства существенно отличают БДС от других систем, изучаемых в физике, химии или технике. Перечислим их:

1. Во-первых, БДС – это системы с компартментной и кластерной структурой, когда отдельная (условно!) единица – компартмент – может состоять из одного элемента или целого множества, но при этом важна динамика поведения такого множества (компартмента или кластера – совокупности компартментов). Такой компартментно-кластерный подход (ККП) уже заложен в строении воды (без всяких добавок и компонент, но образующей основу любой БДС). Сейчас требуется переосмысливание значимости ККП для новой теории строения и свойств воды (и всех биосистем) путем перехода от термодинамики сплошных сред (с их уравнениями теплопроводности, диффузии и вязкости) к работам Е.П. Хижняка, Г.Р. Иваницкого и их коллег [179] по кластерному строению воды. И здесь также требуются новые методы измерений и новые модели на основе этих измерений. При этом очевидно, что такие кластерные БДС являются сложными, иерархическими системами и их придется описывать многокомпонентными векторами 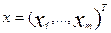в m-мерном фазовом пространстве состояний (ФПС) и для таких БДС уже имеются определенные теории, одну из которых автор последние 20 лет неоднократно уже представлял [61-93]. Синергетической особенностью ККП является требование системного синтеза, т.е. минимизации размерности фазового пространства, перехода от m к k, где k<<m. Измерение параметров порядка для БДС и минимизация размерности ФПС уже решалась автором для БДС, находящихся в квазистационарных состояниях, но задача эта крайне сложная в общем случае [26,43,174,176,187,199,200,204,218,219,231,233].

2. Второй очень неприятной особенностью БДС (и это начинается уже от кластеров обычной воды, как показал Е.П. Хижняк [179]) является постоянное изменение структуры и связей, т.е. БДС относятся к кластеру «glimmering system», т.е. «мерцающим системам». Причем это «мерцание» относится не только к изменению величин параметров вектора состояния системы – ВСС, но и к размерности ФПС, к значимости x_i (сейчас эти x_i – параметры порядка, а чуть позже – уже нет, ими становятся другие). Работать с такими «мерцающими системами» очень сложно, для них нет аналогов в физике или химии, т.к. термин «флуктуация» в этих точных науках имеет уже укоренившееся значение и смысл, и можно только весьма условно его использовать для БДС, т.е. говорить о «биофлуктуациях» БДС. При этом нужно вкладывать в это понятие некоторый другой, биологический смысл (хотя бы в смысле «glimmer»). При этом, используя термин «биофлуктуация», мы будем говорить о постоянном изменении не только величин x_i, но и размерности m в ФПС, изменения параметров порядка и т.д.. И что особенно неприятно в этой попытке проведения аналогии с физикой, так это отсутствие возможностей флуктуировать вблизи средних значений, т.е. распределение в некотором объеме ФПС (мы его будем в дальнейшем называть квазиаттрактором) может быть (и, как правило, бывает) равномерным. В этом аспекте автор ставит глобальный вопрос о распределении параметров ВСС в ФПС: мы имеем дело с равномерным или неравномерным распределением для биосистем? Доказательства того или другого сейчас существуют.

3. Такие сложные, «мерцающие» БДС при этом обладают еще и эволюцией. Мы говорим о микроэволюции человека (как пример одной из 3-х БДС в ФПС от рождения до старости и смерти) или об эволюции человечества (переход от традиционалистского типа к технологическому обществу и далее в знаниевое, синергетическое, постиндустриальное общество – ЗСПО). Микро- или макроэволюция присущи любой БДС, и в этом еще одна сложность (как прогнозировать динамику и конечное состояние этой эволюции).

4. Все БДС обладают свойством телеологичности. Возможно, в это понятие следует вкладывать другой смысл, чем это делал Л. фон Берталанффи, но некоторая конечная цель в динамике развития любой БДС имеется. Например, для человека – это процесс накопления информации для себя и для человечества (если этот человек – ученый) или неизбежность смерти человека, а может быть и всего человечества (!?). Все это еще предстоит изучать, но эти свойства явно обозначаются в динамике любой БДС (в частности, и для функциональных систем организма – ФСО).

5. Самое экстравагантное свойство БДС и тяжело воспринимаемое сторонниками детерминистско-стохастического­ подхода – это свойство выхода за пределы трех сигм (для распределения Гаусса попадание за эти границы имеет вероятность P<0,003). Принципиально, что БДС, вся эволюция живого происходит за пределами 3-х сигм, т.е. имеют место гигантские «биофлуктуации», отклонения от средних значений. Именно такие БДС, в частности, люди (гении) создают новые (тоже экстравагантные, выходящие далеко за интервалы устоявшихся границ) теории и подходы, новые направления в науке. Все биологические процессы, выходящие за пределы 3-х сигм, должны регистрироваться, изучаться, измеряться и для них необходимо строить модели в рамках новой ТХС.

Учитывая сложность и неоднозначность (сравнительно с техникой, физикой и химией) понятий и трактовок в изучении БДС, а также необходимость перехода от ДСП к ТХС в естествознании в целом и в медико-биологических науках в частности, возникает проблема разработки новых подходов в выполнении измерений БДС и их моделирования. Для автора настоящего сообщения и его коллег сейчас очевидно, что одной только компартментно-кластерной теорией биосистем (ККТБ) обойтись не удастся, хотя она и использует все постулаты Г. Хакена [181], но не учитывает количественно выше обозначенные свойства БДС со 2-го по 5-е (см. выше). Именно для изучения БДС, измерения и оценки их параметров нужны другие подходы и средства измерений и расчетов, которые бы учитывали все 5 свойств БДС. Сейчас такие попытки предпринимаются многими авторами и один из вариантов решения указанной проблемы базируется на измерениях характера движения вектора состояния биосистемы (ВСБС) и, в частности, вектора состояния организма человека (ВСОЧ) в ФПС. В рамках этого подхода учитывается кластерность БДС (с помощью m -мерного вектора), свойства «мерцания», микроэволюция БДС, телеологичность и учет огромных разбросов параметров БДС, которые, как мы показали, могут нести существенную информацию о состоянии БДС, ее эволюции и конечном состоянии. Именно учет изменчивости (или вариабельности) параметров БДС (вместо термина «флуктуации», принятого в физике, химии и технике) оказывается весьма информативным параметром для построения моделей биосистем и сравнения различных состояний биосистем в медико-биологических исследованиях. В целях систематизации выделим наиболее важные различия (параметры перехода) между ДСП и СП, которые представлены в таблице 5.2. Отметим, что она существенно отличается от табл. 1.1 стр.16 [181] и расширяет особенности СП.

Таблица 5.2

Различия в подходах между детерминистско- стохастической парадигмами (ДСП) и синергетической парадигмой (СП)

ДСП в описании движения вектора состояния системы – ВСС	СП в описании движения вектора состояния системы
1.Изучаются поведения отдельных элементов	1.Изучаются не отдельные элементы, а пулы, компартменты, кластеры (по Г. Хакену)
2.В формальном аппарате (в фазовом пространстве состояний - ФПС) работаем с точками или линиями	2.В ФПС работаем с областями ФПС, внутри которых движется вектор состояния системы (эти области - облака - образуют квазиаттракторы)
3.Имеются стационарные режимы (для вектора состояния x имеем dx/dt=0 и x=const)	3.Не имеются стационарные режимы (dx/dt≠0 и x≠const), т.к. система находится в постоянном движении в ФПС (она обладает свойством “glimmering system”)
4.Системы иногда имеют компартментно-кластерную структуру (ККС)	4.Многие системы имеют ККС
5.Некоторые системы телеологичны (имеют прогнозируемое конечное состояние)	5. Многие системы (человекомерные) имеют телеологические свойства (прогнозируемое конечное состояние)
6.Некоторые системы эволюционируют	6.Все человекомерные системы эволюционируют
7.Выход за пределы 3-х сигм - артефакт и не изучается	7.Выход за пределы 3-х сигм - закономерность и активно изучается (влияет на параметры квазиаттракторов)
8.Распределения параметров ВСС неравномерные	8.Обычно распределения параметров ВСС равномерные
9.Хаотические режимы эпизодические и они моделируются ДСП моделями	9.Система постоянно находится в микрохаосе и этот микрохаос описывается квазиаттрактором, ДСП- моделей нет
10.Единица (элемент) характеризует динамику процесса в рамках системного анализа	10.Единица - ничто и единица - всё (если она параметр порядка) в рамках системного синтеза (главная проблема СП)
11.Обычно размерность ФПС (модели) не изменяется, мониторинг системы не требуется, т.к. априори есть модели или функции распределения для ВСС	11.Размерность m ФПС изменяется легко, поэтому требуется постоянный мониторинг параметров порядка для ВСС
12.В теории хаоса (подход И.Р. Пригожина и В.И. Арнольда) начальное состояние задано определённо	12.Начальное состояние не определено (известны приблизительно параметры квазиаттрактора)
13.Параметры модельных квазиаттракторов могут быть определены точно	13.Параметры реальных (точнее идеальных) аттракторов никогда не могут быть определены (квазиаттракторы приблизительно представляют реальные аттракторы как частота события, его вероятность), но из-за 5-ти свойств биосистем реальные аттракторы никогда не достижимы

В этой связи отметим также определённую возможность количественной оценки свойств и параметров БДС в рамках учёта всех пяти указанных свойств. Для такой количественной оценки свойств и параметров БДС введем ряд постулатов (предложений), которые образуют базу для моделирования человекомерных систем.

1. Любая БДС может описываться вектором состояния 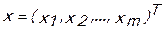, в m -мерном фазовом пространстве состояний (ФПС). Компонентами этого вектора, вообще говоря, могут быть любые переменные: параметры кардиореспираторной системы (КРС), биохимические параметры крови, параметры различных физиологических и психофизиологических функций человека и т.д. При этом главное, что существуют методы и приборы для их объективного измерения. Об этом автор уже говорил в более ранних работах [26,60-82,287-235], когда, например, строились и измерялись параметры моделей респираторных нейронных сетей (или других нейросетей) в рамках компартментно-кластерного подхода (там, в качестве x_i,была биоэлектрическая активность эфферентных нервов или мышц) [61].

2. Имея максимальный набор x_i всегда можно минимизировать размерность ФПС, т.е. перейти от m к k, где k<m (или k<<m). Сейчас в лабораториях при СурГУ такие процедуры разработаны для разных БДС. Эти процедуры позволяют минимизировать размерность фазового пространства и получить некоторую компактную модель исследуемой БДС. Для этих целей сейчас используются три подхода: минимизация размерности ФПС в рамках ККТБ, использование нейросетевых технологий и метод анализа параметров квазиаттракторов движения ВСОЧ в ФПС. Последний базируется на третьем постулате, но дает реальную оценку значимости x_i [232-235].

3. Уровень изменчивости (интенсивность разброса ВСБС в ФПС, как некий аналог флуктуациям в физике) параметров БДС (значений x_i в ФПС) является информацией для оценки состояния биосистем и прогноза их перехода в другие состояния (в другие области фазового пространства, замены параметров порядка, вообще перехода в другие ФПС). Существенно, что уровень изменчивости БДС является измеряемой величиной и он может длительно мониторироваться, сравниваться для разных групп биосистем или для одной и той же биосистемы, но находящейся в разных функциональных состояниях [61,90-93,162-164].

Дата добавления: 2015-10-23