Лабораторна робота К–6

Вивчення електричного резонанса

Мета роботи: зняття резонансних кривих коливального контуру та перевірка формули Томсона.

Коло, складене з ємності C, індуктивності L та активного опору R, має назву коливального контура.

Якщо зарядити конденсатор, а потім дати йому можливість розрядитися через котушку, в контурі виникнуть електромагнітні коливання, що обумовлені переходом енергії електричного поля електричного конденсатора в енергію магнітного поля котушки та назад. У випадку, коли опір контура R=0, коливання будуть мати незатухаючий харак­тер. Наявність омічного опору приведе до поступового затухання коливань, оскільки частина енергії буде витрачатися на нагрівання проводів та котушки індуктивності. Період цих коливань

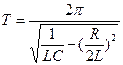. (1)

Якщо омічний опір R кола дуже малий, а індуктивний опір не малий, ми будемо мати повільно затухаючі коливання. При цьому в формулі (1) можна знехтувати в знамен­нику величиною 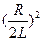в порівнянні з . Тоді для періоду таких коливань отримаємо т.з. формулу Томсона:

. (2)

Якщо коливальний контур в якому-небудь місці розірвати та до розриву, що утворився, підключити джерело зовнішньої змінної ЕРС, то під дією цієї зовнішньої ЕРС в контурі виникають вимушені коливання (мал.1).

Якщо зовнішня ЕРС змінюється періодично за законом

(3)

то і вимушені коливання будуть синусоїдними. Рівняння вимушених коливань (на підставі другого закону Кірхгофа для квазістаціонарного струму) запишеться у вигляді

(4)

де – падіння напруги на індуктивності;

RI – падіння напруги на активному опорі;

– падіння напруги на ємності;

q – заряд на обкладках конденсатора.

Частинний розв‘язок диференціального рівняння має вигляд

, (5)

т.т. показує, що сила струму буде змінюватися з тією ж частотою w, що й вимушена ЕРС.

Повний розв‘язок містить ще й вираз

I₀e^-btsinwt,

що представляє собою затухаючі коливання, які швидко припиняються.

Амплітуда струму буде

(6)

та досягає максимуму при

або . (7)

З формули (1) видно, що циклічна частота власних коливань контуру

, (8)

т.т. дещо менше, ніж циклічна частота вимушених коливань при резонансі. При нескін­ченно малому опорі R резонанс наступає при частоті, рівній частоті власних коливань кола.

При резонансній частоті амплітуда сили струму І₀ набуває максимального значення:

.

Вона тим більше, чим менше омічний опір R. На мал.2 наведено декілька резонансних кривих, що відповідають різним значенням R. Чим менше R, тим гостріше максимум.

Падіння напруги на омічному опорі

U_R=IR=I₀Rsin(t-j) (9)

на індуктивному – (10)

на ємнісному – (11)

З останніх двох виразів видно, що u_C зсунуте на p по відношенню до u_L, т.т. напруги на ємності та індуктивності мають протилежні фази S.

З рівнянь (10) та (11) випливає, що амплітудні значення напруг на індуктивності L та ємності С рівні:

U_0L=LI₀; (12)

. (13)

У випадку резонансу, та рівняння (12), (13) набудуть вигляду

, (14)

де w=2pn – циклічна частота.

Так як при резонансі , то U_OL=U_OC, т.т. напруги на ємності та індуктивності однакові за величиною. Але оскільки вони протилежні за фазою, то сумарна напруга

u_C+u_L=0.

Якщо, крім цього, , то, як видно з виразів (13) та (14), напруга на ємності та індуктивності більше, ніж e₀. Цей випадок має назву резонансу напруг.

Крім цього можливий резонанс струмів. Він виникає у випадку контуру, приєд­наного до джерела зовнішньої ЕРС паралельно. При резонансі струмів в підвідних дротах струм буде значно слабше в окремих гілках контуру.

Дата добавления: 2015-10-23