Лабораторна робота К–5

Визначення величини магнітного моменту лінійного магніту методом Гауса.

Мета роботи: вивчення методу крутильних коливань, що застосовується для визначення магнітного моменту постійного магніту.

На лінійний магніт, розташований в однорідному магнітному полі, діє обертальний момент, який намагається встановити ось магніту в напрямку індукції (або напруженості) цього поля (мал.5-1)

Величина обертального моменту пропорційна індукції В зовнішнього поля, синусу кута a між напрямками осі магніту та зовнішнього магнітного поля та залежить від властивостей даного магніту:

M=PBsina

де Р – магнітний момент магніту.

Звідси видно, що магнітний момент чисельно дорівнює обертальному моменту пари, що діє на даний магніт в полі, індукція якого дорівнює одиниці, при куті, рівному p/2, між напрямками осі магніту та зовнішнього поля.

В цій роботі зовнішнім магнітним полем є магнітне поле Землі.

Підвісимо магніт на непружній нитці так, щоб його вісь розташувалась горизон­тально в площині магнітного меридіану Землі. Повернемо його в горизонтальній площині на невеликий кут a, щоб sina»a, та відпустимо. Тоді під дією горизонтальної складової магнітного поля Землі виникнуть коливання магніту в горизонтальній площині.

В цьому випадку вираз для визначення обертального моменту набуде вигляду

М=Рm_оН_ja (1)

(для повітря m=1). З іншого боку, за основним рівнянням динаміки обертального руху, обертальний момент пропорційний кутовому прискоренню:

(2)

де І – момент інерції магніту відносно нитки підвісу.

Знак “мінус” показує, що обертальний момент, обумовлений дією магнітного поля землі на магніт, та кутове прискорення мають протилежні напрямки.

Нитка підвісу вибирається так, щоб її модуль був малим, який дозволяє знехтувати пружними силами, що виникають при крученні. Тому обертальні моменти у виразах (1) та (2) обумовлені дією одних і тих же сил та рівні між собою

звідки (3)

де m_о=1,26*10^-6Гн/м.

Вираз (3) є однорідним диференційним рівнянням гармонічного коливального руху (прискорення пропорційне взятому з протилежним знаком зміщенню), таким чином

, (4)

де w_о=2p/Т – циклічна частота коливань магніту;

Т – період коливань магніту.

Підставивши значення w_о в рівняння (4) та розв’язавши його відносно Т, отримаємо

. (5)

Горизонтальну складову магнітного поля Землі Н_j визначену за допомогою бусолі. Для цього встановимо бусоль в даному місці при відсутності магніту. В цьому випадку стрілка бусолі під дією магнітного поля Землі встановиться в площині магнітного меридіану. Потім на спеціальному столику покладемо магніт так, щоб його вісь була перпендикулярна площині магнітного меридіану та знаходилася на одному рівні зі стрілкою бусолі. Стрілка бусолі під дією магнітного поля магніту відхилиться від початкового положення на кут j та встановиться в напрямку Н сумарного поля. На малюнку 5-2 видно, що

, (6)

де Н_м—напруженість магнітного поля, створеного магнітом.

Магніт слід поміщати на достатньо великій відстані від бусолі, щоб магнітне поле його в області стрілки бусолі можна було вважати однорідним.

Величину напруженості магнітного поля магніту на його осі можна визначити, виходячи з еквівалентності полів котушки та магніту. Відомо, що напруженість магніт­ного поля кругового струму на його осі виражається формулою

.

де R – радіус витка;

r – відстань вздовж осі від центра цього витка до точки, в якій визначається напруженість.

При r>>R ця формула матиме вигляд

.

де S – площа, що охоплюється круговим струмом.

Якщо магнітне поле створене котушкою з числом витків N, то остання формула матиме вигляд

.

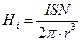Але ISN – магнітний момент котушки, тому

.

Виходячи з еквівалентності магнітних полів котушки та лінійного магніту, можна записати

.

Тут r – відстань вздовж осі магніту від його середини до точки, в якій визначається напруженість.

Підставимо значення H_m в рівняння (6):

.

Підставивши значення H_j в рівняння (5) та розв’язавши його відносно Р, отримаємо

(7)

Дата добавления: 2015-10-23