Лабораторна робота К–3

Визначення логарифмічного декремента та коефіцієнта затухання механічних коливань.

Мета роботи: визначення логарифмічного декремента та коефіцієнта затухання механічних коливань.

Коливання з амплітудою, яка неперервно зменшується, називаються затухаючими.

Логарифмічний декремент та коефіцієнт затухання коливань є одними з най­важливіших характеристик будь-якого тіла, що здійснює затухаючі коливання. Тіло буде здійснювати затухаючі коливання, якщо на нього крім квазіпружньої сили f_кв=-kх буде діяти сила тертя (опору), яка при малих амплітудах пропорційна швидкості тіла, яке коливається:

;

де х – зміщення тіла, що коливається в положенні рівноваги;

к – коефіцієнт квазіпружньої сили;

r – коефіцієнт сили тертя (коефіцієнт опору).

Якщо застосувати ІІ закон Ньютона

до тіла масою m, на яке діє квазіпружня сила та сила тертя, отримаємо диференційне рівняння затухаючих коливань

, (1)

де ;

b – коефіцієнт затухання, що характеризує швидкість затухання коливань;

w_о – частота, з якою здійснювалися би вільні коливання тіла при відсутності опору середовища (при r=0), цю частоту називають власною частотою системи.

При не дуже сильному затуханні, коли b<w_о, загальний розв’язок рівняння (1) має вигляд

х=А_ое^-btcos(wt+j), (2)

де А_о – початкова амплітуда коливань;

j – початкова фаза;

w – циклічна частота затухаючих коливань.

В рівнянні (2)

A_t=A_oe^-bt (3)

— амплітуда затухаючих коливань.

Часто швидкість затухання коливань характеризують не коефіцієнтом затухання b, а величиною, з ним пов’язаною, – логарифмічним дикрементом затухання l, що являє собою натуральний логарифм суми відношення двох послідовних амплітуд, що взяті через проміжок часу, рівний періоду коливань, т.т.

. (4)

Експериментально коефіцієнт затухання b легко можна знайти, якщо виміряти проміжок часу t₂, протягом якого амплітуда коливань зменшується вдвічі, т.т. А_t=1/2А_о.

З врахуванням (3) запишемо

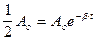, або ln2=bt₂,

звідки

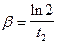. (5)

Підставивши (5) в (4), отримаємо

. (6)

Формули (5) та (6) дозволяють обчислити коефіцієнт та логарифмічний декремент затухання маятника та камертона.

Дата добавления: 2015-10-23