Приклади дослідження невласних інтегралів на абсолютну та умовну збіжність.

Приклад 1. Дослідити на абсолютну та умовну збіжність інтеграл

.

Зробимо заміну змінної 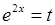, тоді , , тому

. (13.1)

Функція обмежена, а функції та монотонно прямують до нуля при , отже обидва інтеграли в (13.1) збіжні за ознакою Діріхле, отже інтеграл збіжний. Покажемо, що інтеграл , де , розбіжний. Дійсно, при ; .

Розглянемо інтеграл . Перший з цих інтегралів розбіжний, а другий збіжний за ознакою Діріхле, отже інтеграл розбіжний. Тоді за теоремою 2 інтеграл розбіжний, отже інтеграл збігається умовно.

Приклад 2. Дослідити на абсолютну та умовну збіжність інтеграл Френеля:

.

Маємо: , де , . Інтеграл – звичайний власний інтеграл Рімана, тому питання про збіжність інтеграла рівносильне питанню про збіжність інтеграла . В інтегралі зробимо заміну: . Тоді , , отже

.

Звідси видно, що цей інтеграл збіжний за ознакою Діріхле (функція 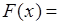обмежена, а функція монотонно прямує до нуля при ). Покажемо, що він збіжний умовно. Дійсно, оскільки , а інтеграл розбіжний (див. п. 11, приклад 1), то розбіжним є інтеграл 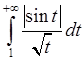, отже інтеграл збіжний умовно, а тоді збіжний умовно й інтеграл .

Аналогічні висновки стосуються й другого інтеграла Френеля .

Приклад 3. Дослідити на абсолютну та умовну збіжність інтеграл

.

Пригадаємо (п. 10, приклад 5), що інтеграл

збігається при та при , і розбіжний при всіх інших .

Розглянемо окремо випадки.

1) . Оскільки , а інтеграл збігається, то інтеграл збігається абсолютно.

2) . Також інтеграл збігається абсолютно.

3) . Оскільки , і функція обме-

жена, то інтеграл збігається за ознакою Діріхле. Розглянемо:

.

Перший з цих інтегралів розбіжний (обчислюється безпосередньо), а другий збіжний (за ознакою Діріхле). Таким чином інтеграл розбіжний, отже інтеграл збігається умовно.

4) . Оскільки , і функція об-

межена, то інтеграл збіжний за ознакою Діріхле. Розглянемо:

.

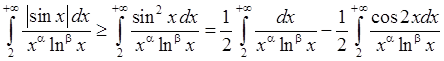Перший з цих інтегралів розбіжний, а другий збіжний (за ознакою Діріхле), отже інтеграл збіжний умовно.

5) . Інтеграл збіжний за ознакою Діріхле (функція моно-

тонно прямує до нуля при , функція обмежена).

Розглянемо:

.

Перший з цих інтегралів розбіжний, а другий збіжний за ознакою Діріхле, отже інтеграл збіжний умовно.

6) . У цьому випадку отримуємо інтеграл , який, оче-

видно, розбіжний.

7) . Позначивши , запишемо у вигляді:

.

Доведемо наступний результат. Нехай функція неперервна та додатна на , . Тоді інтеграл розбіжний.

Скористаємось критерієм Коші. Покажемо, що існує таке, що для будь якого знайдуться такі, що

. (13.2)

Візьмемо для довільного натуральне число 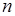так, щоб . Тоді , і покладемо , 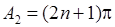. Оскільки на відрізку функція не змінює знаку та інтегровна, то на підставі теореми про середнє значення існує таке, що

.

Тоді

.

Оскільки , , то . Отже завжди можна обрати 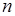настільки великим, щоб . І тоді рівність (13.2) виконано, тобто згідно критерію Коші інтеграл розбіжний. З цього результату одразу ж випливає розбіжність інтеграла , оскільки функція при неперервна, додатна, і .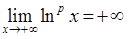

8) . Позначивши , запишемо інтеграл у вигляді:

.

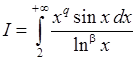Функція 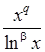при та неперервна, додатна, і . Тому на підставі того ж твердження, інтеграл розбіжний.

Отже остаточно, інтеграл

при збігається абсолютно ;

при збігається абсолютно;

при збігається умовно;

при збігається умовно ;

при збігається умовно;

при розбігається;

при розбігається .

Дата добавления: 2015-10-30