Задачі, що приводять до поняття визначеного інтеграла.

ВИЗНАЧЕНИЙ ІНТЕГРАЛ

ТА ЙОГО ЗАСТОСУВАННЯ

Конспект лекцій

по курсу математичного аналізу

для студентів I курсу фізичного факультету

(спец. прикладна фізика)

Одеса, 2013

Задачі, що приводять до поняття визначеного інтеграла.

У багатьох сферах людської діяльності з давнини виникала необхідність обчислювати метричні характеристики різних геометричних фігур, як то довжини дуг ліній, площі фігур, об’єми тіл тощо. Такі задачі легко розв’язувалися для простих геометричних фігур, таких як квадрати, трикутники, паралелограми, трапеції. Площу многокутника можна було обчислити розбиттям його на трикутники і знаходженням суми площ цих трикутників. Всі ці фігури утворювались за допомогою відрізків прямих ліній. Але задача набагато ускладнюється, якщо мова йдеться про обчислення площ криволінійних фігур, наприклад площі круга. Давні єгиптяни наближено обчислювали цю площу за допомогою формули:

, де – діаметр круга, а –його радіус (порівняйте з тепер відомою точною формулою ; ). Греки зводили обчислення площі круга до побудови квадрата, який має ту саму площу. Але за допомогою циркуля та лінійки ця задача ніяк не розв’язувалася. І лише наприкінці XIX століття (у 1882 році) німецьким математиком Карлом Ліндеманом було доведено, що ця задача не має розв’язку.

Рис. 1.

Значний внесок у розв’язання проблеми про площу круга зробив видатний грецький математик IV ст. до н.е. Євдокс Книдський. Він вписував в круг правильний многокутник, а потім доводив, що за рахунок збільшення кількості сторін многокутника (відповідно зменшенням їх довжин) можна добитися того, щоб його площа як завгодно мало відрізнялась від шуканої площі круга (рис. 8.1). Цей метод отримав назву метода вичерпання. В цьому доведенні нібито вичерпується простір між многокутником та колом, яке обмежує круг. По суті справи Євдокс підійшов до поняття границі – основи всієї вищої математики.

Дуже важливий крок далі зробив славнозвісний Архімед (287–212 рр. до н.е.). Він знайшов загальні методи відшукання площ криволінійних фігур і застосував їх до обчислення кругових, параболічних та багатьох інших фігур. Основа всіх цих методів полягала все у тому ж – а саме шукана площа криволінійної фігури знаходилась як границя площ вписаних в неї прямолінійних фігур.

Потім з’ясувалось, що аналогічний підхід можна застосувати не тільки для розв’язання геометричних задач, а й задач з області механіки, фізики тощо. Свій подальший розвиток ця теорія отримала у працях Й.Кеплера (1598–1647), П.Ферма (1601–1665), Дж.Валліса (1616–1703), Б.Паскаля (1623–1662) та деяких інших вчених. Цікаво, що Кеплер зіткнувся з цими проблемами, коли йому треба було обчислювати об’єми бочок для вина. Не треба тем не менш звідси робити висновок, що алкоголь сприяє розвитку науки.

Спільним для всіх цих робіт було те, що шукана величина наближено замінювалась сумою великого числа малих величин, кожна з яких обчислювалась легко. Це було поступове створення інтегрального зчислення, яке набуло свого основного завершення у працях І.Ньютона (1643–1727) і Г.Лейбніца (1646–1716).

Перейдемо тепер до точних математичних формулювань.

1. Задача про площу криволінійної трапеції.

Нехай на відрізку задано функцію . Фігура, яка обмежена графіком даної функції і відрізками прямих називається криволінійною трапецією (рис. 2).

Рис. 2.

Треба обчислити площу цієї трапеції. Зауважимо, що у загальному випадку ця трапеція – саме криволінійна фігура, і лише у частинних випадках, коли функція стала, або лінійна (тобто її графіком є пряма лінія) ця фігура прямолінійна, і ми можемо використати відомі з елементарної геометрії формули для площ прямокутника та трапеції.

Розіб’ємо відрізок за допомогою довільно обраних точок

на 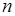частинних відрізків . На кожному з них візьмемо довільну точку і побудуємо прямокутник, основою якого є відповідний частинний відрізок, а висота дорівнює (рис.3).

Рис. 3.

З рис. 3 ми бачимо, що шукана площа наближено дорівнює сумі площ всіх отриманих прямокутників. Знайдемо цю суму. Очевидно, вона дорівнює:

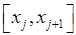, де – довжина відрізка . Тобто . За рахунок чого можна було б збільшити точність цієї формули? Здавалось би за рахунок збільшення кількості частинних відрізків, тобто числа 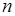. Але справа в тому, що кількість прямокутників можна збільшувати не на всьому відрізку , а тільки на деякій його частині (наприклад половині його), залишаючи кількість частинних відрізків на решті відрізка незмінним. І тоді очевидно, що ми не отримаємо підвищення точності. Тому треба йти іншим шляхом. А саме зменшувати всі величини . Фактично можна зменшувати . 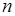Зрозуміло, що тоді автоматично буде збільшуватися. І за площу криволінійної трапеції природно вважати границю послідовності площ ступінчатих фігур, якщо максимальна з довжин частинних відрізків прямує до нуля:

. (1.1)

2. Задача про роботу змінної сили.

Нехай вздовж осі діє сила , напрям якої сталий і збігається з напрямком . Крім того сила може змінюватись за величиною. Нехай під дією сили матеріальна точка перемістилася вздовж осі з точки у точку . Треба обчислити роботу цієї сили на відрізку .

Відомо, що якщо сила стала () і діє у напрямку переміщення, то робота дорівнює добутку величини сили на величину переміщення:

.

Але сила змінна, і ми не маємо права користуватися цією формулою. Тому розіб’ємо відрізок точками на частинні відрізки і припустимо, що кожний частинний відрізок 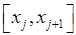настільки малий, що сила не встигає на цьому відрізку суттєво змінитися, та її можна на ньому вважати сталою. Оберемо на кожному з відрізків довільну точку , тоді на 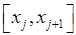виконано: . Робота, що виконана цією силою на відрізку 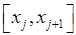, дорівнює , де . Тоді робота на всьому відрізку наближено дорівнює:

.

Ця наближена рівність тим точніша, чим менші довжини . Тому природно за роботу сили на шляху вважати границю:

.

Звернемо увагу на те, що ми отримали формулу, яка повністю аналогічна формулі (1.1). Таким чином дві задачі з різних галузей науки привели до однієї математичної формули. Таку особливість математики ми вже відмічали вище.

Дата добавления: 2015-10-30