Формула Ньютона–Лейбніца.

Нехай функція інтегровна на відрізку . Візьмемо довільне , тоді функція буде інтегровна на відрізку , тобто існує інтеграл

.

Якщо змінюється, то відповідним чином буде змінюватись і цей інтеграл, тобто він являється функцією змінної . Позначимо цю функцію через :

. (5.1)

Інтеграл (5.1) називається інтегралом зі змінною верхньою межею.

Теорема 1. Якщо функція інтегровна на відрізку , то функція неперервна на цьому відрізку.

Доведення. Нехай , . Покажемо, що

.

Внаслідок формули (4.1) маємо:

.

Оскільки функція інтегровна на відрізку , то вона обмежена на цьому відрізку, тобто

.

Тоді на підставі властивостей 10, 11 інтеграла (див. п. 4) звідси випливає, що

,

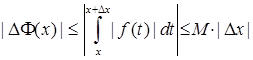звідки отримуємо, що при , тобто функція неперервна в точці . Оскільки – довільна точка відрізку , то функція неперервна на всьому відрізку .

Теорема 2. Похідна інтеграла зі змінною верхньою межею від неперервної функції дорівнює значенню підінтегральної функції для цієї межі, тобто:

.

Доведення. Нехай функція неперервна на відрізку . Тоді вона інтегровна на цьому відрізку. За означенням похідної маємо:

.

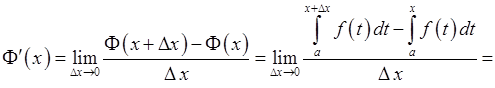
Згідно з теоремою про середнє значення, внаслідок неперервності функції на відрізку 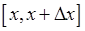існує така точка , що справджується рівність:

.

Тоді

.

Оскільки , то , і тому внаслідок неперервності функції :

, і теорему доведено.

Ця теорема має дуже важливе значення. Вона стверджує існування первісної у будь якої неперервної функції і встановлює зв’язок між невизначеним і визначеним інтегралами. Функція є первісною для функції , отже

.

На підставі доведеної теореми легко отримується славнозвісна формула Ньютона–Лейбніца*.

Нехай 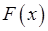– будь яка первісна функції на відрізку . Оскільки також первісна для функції , то

.

Покладемо тут . Оскільки

,

то , звідки , тобто

.

Покладемо тут 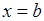. Дістанемо:

, або, що те ж саме:

. (5.2)

Це й є формула Ньютона–Лейбніца, яку називають основною формулою інтегрального зчислення. Її значення важко переоцінити, тому що вона дає зручний засіб обчислення інтегралів без використання інтегральних сум. Правда те, що вона справедлива лише для неперервних функцій, дещо звужує її можливості. Крім того, слід пам’ятати, що існують функції, первісні від яких не виражаються елементарними функціями. Тоді можливості застосування формули Ньютона–Лейбніца також обмежуються.

Дата добавления: 2015-10-30