Обчислення об’ємів тіл.

Розглянемо деяке тіло (рис. 19) 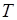. Позначимо через площу перерізу цього тіла площиною, яка проходить перпендикулярно деякій осі через точку з координатою 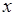на цій осі .

Розіб’ємо відрізок на частинні відрізки точками:

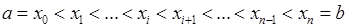
Рис. 19.

і проведемо через ці точки площини, перпендикулярні відрізку . На кожному з частинних відрізків 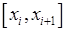оберемо довільну точку . Площини розбивають наше тіло 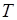на елементарні циліндри . Площа основи циліндра дорівнює 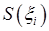, а висота 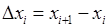. Сумарний об’єм всіх циліндрів:

.

Границя цієї суми при 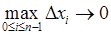(якщо вона існує) називається об’ємом даного тіла. Очевидно, що – це інтегральна сума для функції 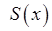, отже об’єм тіла :

.

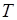Таким чином доведено формулу:

. (16.1)

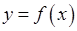Розглянемо, зокрема, об’єм тіла, яке утворено обертанням фігури, обмеженої графіком функції , відрізком осі та прямими та , навколо осі (рис. 20).

Рис. 20.

Тоді площа перерізу , і згідно з формулою (16.1):

. (16.2)

Якщо така ж сама фігура обертається навколо осі , то можна довести, що об’єм утвореного тіла дорівнює:

. (16.3)

Нехай тепер рівняння лінії, що обмежує нашу фігуру, задано у параметричній формі: , , , причому функція припускається неперервно диференційовною, а функція – неперервною на відрізку . Тоді, якщо фігура обертається навколо осі , то об’єм утвореного тіла дорівнює:

. (16.4)

Якщо та ж сама фігура обертається навколо осі , то об’єм утвореного тіла дорівнює:

. (16.5)

Нарешті розглянемо у полярній системі координат фігуру, яку обмежено променями , (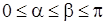) та графіком функції . Тоді об’єм тіла, утвореного обертанням цієї фігури навколо полярної осі, дорівнює:

. (16.6)

Приклади.

1. Знайти об’єм еліпсоїда

.

У перерізі еліпсоїда площиною, паралельною площині на відстані

від неї утворюється еліпс:

,

або:

.

Півосі цього еліпса , і його площа дорівнює (див. приклад після формули (14.2)):

.

Тому за формулою (16.1) маємо:

(перевірте самостійно). Зокрема, якщо , дістаємо формулу об’єму кулі:

.

2. Знайти об’єм тіла, утвореного обертанням графіка функції навколо відрізка осі .

За формулою (16.2) маємо:

.

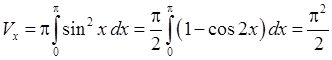3. Знайти об’єм тіла, утвореного обертанням фігури, обмеженої графіком функції , відрізком осі , та прямими , : а) навколо осі ; б) навколо осі .

Об’єм тіла, утвореного обертанням даної фігури навколо осі , знайдемо за формулою (16.2):

.

Об’єм тіла, утвореного обертанням тієї ж фігури навколо осі , знайдемо за формулою (16.3):

.

4. Знайти об’єм тіла, утвореного обертанням фігури, обмеженої аркою циклоїди , , навколо: а) осі ; б) осі .

Об’єм тіла, утвореного обертанням навколо осі , знайдемо за формулою (16.4):

.

Об’єм тіла, утвореного обертанням навколо осі , знайдемо за формулою (16.5):

(обчислення інтегралів перевірте самостійно).

5. Знайти об’єм тіла, утвореного обертанням фігури, обмеженої кардіоїдою , , навколо полярної осі.

Внаслідок симетрії кардіоїди відносно полярної осі (рис. 14), тіло, яке утворено обертанням всієї кардіоїди навколо полярної осі, співпаде з тілом, яке утворено обертанням тільки верхньої половини кардіоїди, яка відповідає зміні кута від до . Тоді, користуючись формулою (16.6), дістанемо:

.

Дата добавления: 2015-10-30