Обчислення площ плоских фігур.

Визначений інтеграл має чисельні застосування у багатьох галузях знань – у геометрії, фізиці, механіці, хімії, біології, економіці та інших. Тут ми розглянемо застосування визначеного інтеграла для розв’язання деяких геометричних задач.

1. Обчислення площ плоских фігур у прямокутній декартовій системі

координат.

Розглянемо фігуру, яка обмежена графіками функцій 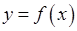та ,де – неперервні на відрізку функції, на відрізку , а також вертикальними прямими (рис. 8.6).

Виходячи з геометричного змісту визначеного інтеграла, можемо стверджувати, що площа фігури ABCD дорівнює різниці площ двох криволінійних трапецій:

. (14.1)

Рис. 8.

Приклади.

1. Обчислити площу фігури, яку обмежено лініями (рис. 9).

Рис. 9.

На підставі формули (14.1) маємо:

.

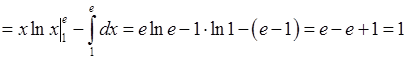2. Обчислити площу фігури, яку обмежено графіками функцій , 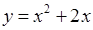(рис. 10).

Рис. 10.

Знайдемо спочатку межі інтегрування, як абсциси точок перетину графіків функцій , 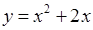. Дорівняємо:

Або . Розв’язуючи це квадратне рівняння, отримаємо:

.

Отже

.

2. Обчислення площі фігури, обмеженої лініями, які задані параметрично.

Нехай криволінійна трапеція обмежена кривою, заданою параметрично:

,

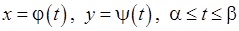де – неперервні і неперервно диференційовні на проміжку функції. Якщо функція монотонна на і , , то площа криволінійної трапеції обчислюється за формулою:

. (14.2)

Приклад. Обчислити площу, обмежену еліпсом , (рис. 11).

Рис. 11.

Очевидно, що шукана площа може бути знайдена як помножена на 4 площа її частини, що розташована у першому квадранті, адже еліпс – фігура, яка симетрична відносно обох координатних осей. Для цієї частини маємо:

, . Тому:

.

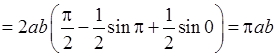3. Обчислення площі фігури у полярній системі координат.

Розглянемо фігуру , обмежену кривою, заданою у полярній системі координат і променями (рис. 12).

Рис. 12.

Така фігура називається криволінійним сектором. Обчислимо його площу. Розіб’ємо відрізок довільно обраними точками

на частинні відрізкі . Фактично це означає, що кут ми розбили на частинні куточки. На кожному з відрізків оберемо довільну точку . І на кожному з частинних відрізків (куточків) побудуємо круговий сектор, який обмежено променями і дугою кола (рис. 13).

Рис. 13.

Площа цього сектора дорівнює:

, де . Сума є інтегральною сумою для функції на відрізку . Отже

.

Таким чином площа криволінійного сектора обчислюється за формулою:

. (14.3)

Приклад. Обчислити площу, обмежену кардіоїдою (рис. 14)

Рис. 14.

Кардіоїда – це траєкторія точки на колі, яке котиться по іншому колу того ж радіуса. Назва цієї лінії походить від грецького слова – серце, її форма нібито нагадує серце. Правда, декому щось інше.

Фігура, обмежена кардіоїдою, симетрична відносно осі , тому її площу можна обчислити як подвоєну площу її верхньої частини. Для неї , тому

.

Дата добавления: 2015-10-30