Задача Коши для волнового уравнения в случае плоских волн.

Полученные точные общие решения волнового уравнения безусловно имеют огромную важность для дальнейшего изучения свойств волнового уравнения. Следующим этапом является постановка и решение задачи Коши для волнового уравнения (1.30.0) в случае плоских волн. Итак, рассматривается уравнение в частных производных второго порядка

, где (1.34.1)

с начальными условиями вида

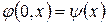(1.34.2)

, где

Наличие в волновом уравнении производной второго порядка по времени обязывает нас ставить начальные условия не только на искомую функцию, но и на первую производную по времени.

Допустим теперь, что решение задачи (1.34.1), (1.34.2) существует, тогда оно дается формулой . Определим функции таким образом, чтобы удовлетворялись начальные условия:

, (1.34.3)

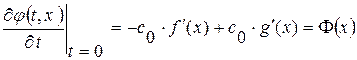, (1.34.4)

Интегрируя второе равенство (1.34.4), получаем ( - постоянные):

(1.34.5)

Рассматривая (1.34.3), (1.34.5) как систему 2-х уравнений относительно 2-х неизвестных находим:

(1.34.6)

Таким образом, мы определили функции через заданные функции , причем равенства (1.34.6) должны иметь место для любого значения аргумента функций . Подставив в формулу общего решения найденные значения (формулы (1.34.6)), получим

или

. (1.35)

Впервые это решение задачи Коши для волнового уравнения получил Л. Эйлер в 1748 г.

Сейчас выполним проверку найденного решения в предположении, что - дважды дифференцируемая функция и - один раз дифференцируемая функция своего аргумента:

1. Решение удовлетворяет волновому уравнению, так как любая дважды дифференцируемая функция и интеграл от один раз дифференцируемой функции от своих аргументов и есть решение волнового уравнения.

2. Решение удовлетворяет начальным данным задачи Коши. Действительно,

, т. е. первое начальное условие выполнено при всех .

Для проверки второго начального условия вспомним формулу вычисления производной от интеграла, зависящего от параметра (правило Лейбница):

, тогда

Что и требовалось доказать. Отметим, что полученное решение вида (1.35) называется формулой Д’ Аламбера и доказывает существование решения поставленной задачи Коши. Эта же формула доказывает и единственность решения. Действительно, если бы существовало второе решение задачи (1.34.1), (1.34.2), то оно представлялось бы формулой (1.35) и совпадало бы с первым решением.

Получим теперь соответствующие найденному решению задачи Коши выражения для возмущений скорости и давления:

(1.34.7)

где символом штрих обозначена обыкновенная производная по переменным , . Найденным выражениям для возмущений скорости и давления соответствуют следующие начальные данные в задаче Коши для искомых функций :

, , где

Дата добавления: 2015-10-23