
|
Читайте также: |
При постановке, анализе и решении многих газодинамических задач (как в рассматри-ваемой нами линейной, так и в общей нелинейной постановке) используется специальный метод 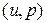 - диаграмм. Эти диаграммы описывают состояния движения
- диаграмм. Эти диаграммы описывают состояния движения 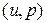 , в которые может перейти данное состояние движения
, в которые может перейти данное состояние движения 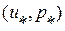 , в результате прохождения какой-либо волны. Где в качестве волны может быть, как мы уже установили выше, либо волна слабого разрыва, получившая название волны разрежения (сжатия), либо волна сильного разрыва - ударная волна. При этом плоскость переменных
, в результате прохождения какой-либо волны. Где в качестве волны может быть, как мы уже установили выше, либо волна слабого разрыва, получившая название волны разрежения (сжатия), либо волна сильного разрыва - ударная волна. При этом плоскость переменных 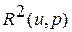 называется плоскостью состояний движения. Дадим два определения:
называется плоскостью состояний движения. Дадим два определения:
Определение1: 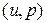 - диаграммой волн разрежения (сжатия) с центром
- диаграммой волн разрежения (сжатия) с центром 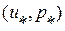 называется геометрическое место точек плоскости состояний движения, изображающих всевозможные состояния
называется геометрическое место точек плоскости состояний движения, изображающих всевозможные состояния 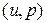 за волнами разрежения (сжатия), имеющими состояние
за волнами разрежения (сжатия), имеющими состояние 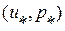 перед волной.
перед волной.
Условия (1.72) на линии (волне) слабого разрыва позволяют без труда получить уравнения 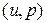 - диаграмм волн разрежения (сжатия) с центром
- диаграмм волн разрежения (сжатия) с центром 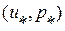 в виде:
в виде:
Для волны разрежения (сжатия), распространяющейся влево (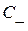 :
: 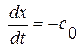 ),
),
 (1.72.1)
(1.72.1)
Для волны разрежения (сжатия), распространяющейся вправо (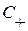 :
: 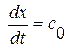 ),
),
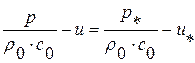 (1.72.2)
(1.72.2)
Графически полная диаграмма волн разрежения (сжатия) представляет из себя пару прямых, проходящих через точку 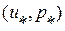 , тангенсы углов наклона которых равны
, тангенсы углов наклона которых равны 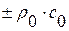 , и изображена на Рис. 1.72. Участки прямых, на которых
, и изображена на Рис. 1.72. Участки прямых, на которых 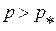 , соответствуют волнам сжатия, а участки, на которых
, соответствуют волнам сжатия, а участки, на которых 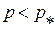 , - волнам разрежения.
, - волнам разрежения.

Рис. 1.72
Определение2: 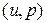 - диаграммой ударных волн с центром
- диаграммой ударных волн с центром 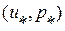 называется геометрическое место точек плоскости состояний движения, изображающих всевозможные состояния
называется геометрическое место точек плоскости состояний движения, изображающих всевозможные состояния 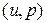 , в которые состояние
, в которые состояние 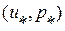 может перейти в ударных волнах. При этом не предполагается, что состояние
может перейти в ударных волнах. При этом не предполагается, что состояние 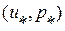 находится перед волной.
находится перед волной.
Условия на сильном разрыве  , где
, где 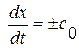 , позволяют без труда получить уравнения
, позволяют без труда получить уравнения 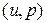 - диаграмм волн разрежения (сжатия) с центром
- диаграмм волн разрежения (сжатия) с центром 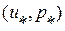 в виде:
в виде:
Для ударной волны, распространяющейся влево (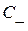 :
: 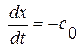 ),
),
 (1.72.3)
(1.72.3)
Для ударной волны, распространяющейся вправо (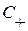 :
: 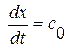 ),
),
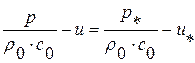 (1.72.4)
(1.72.4)
Графически полная диаграмма ударных волн представляет из себя пару прямых, проходящих через точку 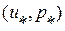 , тангенсы углов наклона которых равны
, тангенсы углов наклона которых равны 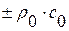 , и изображена на Рис. 1.73. Участки прямых, на которых
, и изображена на Рис. 1.73. Участки прямых, на которых 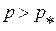 , соответствуют ударным волнам сжатия (УВ сжатия, распространяющаяся вправо (траектория
, соответствуют ударным волнам сжатия (УВ сжатия, распространяющаяся вправо (траектория 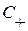 ) и влево (траектория
) и влево (траектория 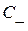 )), а участки, на которых
)), а участки, на которых 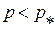 , - ударным волнам разрежения (УВ разрежения).
, - ударным волнам разрежения (УВ разрежения).
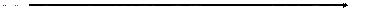
Рис. 1.73
Как уже отмечалось выше, уравнения (1.72.3) и (1.72.4) для случая ударных волн совпадают по написанию с уравнениями (1.72.1), (1.72.2) для случая волн разрежения (сжатия), но описывают при этом разные процессы – в волнах разрежения (сжатия) величины 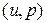 при переходе через фронт волны меняются непрерывно, а в ударных волнах разрежения (сжатия) – разрывно. Причина этого на первый взгляд парадоксального совпадения состоит в следующем – изображенные на Рис. 1.72-73 прямые – суть касательные к кривым
при переходе через фронт волны меняются непрерывно, а в ударных волнах разрежения (сжатия) – разрывно. Причина этого на первый взгляд парадоксального совпадения состоит в следующем – изображенные на Рис. 1.72-73 прямые – суть касательные к кривым 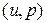 диаграммы для исходной (нелинейной) модели газовой динамики в точке
диаграммы для исходной (нелинейной) модели газовой динамики в точке 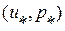 , причем угол наклона этих касательных в точке
, причем угол наклона этих касательных в точке 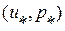 как в случае волн разрежения (сжатия), так и ударных волн одинаков (более того, как вам будет показано в курсе лекций по газовой динамике касание
как в случае волн разрежения (сжатия), так и ударных волн одинаков (более того, как вам будет показано в курсе лекций по газовой динамике касание 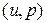 диаграмм простых и ударных волн имеет второй порядок, т. е. кривые имеют не только одинаковый наклон, но и одинаковую кривизну). Аппроксимация исходных нелинейных зависимостей
диаграмм простых и ударных волн имеет второй порядок, т. е. кривые имеют не только одинаковый наклон, но и одинаковую кривизну). Аппроксимация исходных нелинейных зависимостей 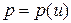 их касательными в окрестности рассматриваемой точки
их касательными в окрестности рассматриваемой точки 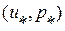 - суть процесса линеаризации исходной нелинейной модели (так называемое акустическое приближение). В ходе этой линеаризации мы приобретаем некоторые свойства не присущие исходной модели, напр., в нелинейной постановке согласно теореме Цемплена для нормальных сред возможны только ударные волны сжатия. В линейной постановке, как мы уже видели, возможны как ударные волны сжатия, так и ударные волны разрежения.
- суть процесса линеаризации исходной нелинейной модели (так называемое акустическое приближение). В ходе этой линеаризации мы приобретаем некоторые свойства не присущие исходной модели, напр., в нелинейной постановке согласно теореме Цемплена для нормальных сред возможны только ударные волны сжатия. В линейной постановке, как мы уже видели, возможны как ударные волны сжатия, так и ударные волны разрежения.
Рассмотрим в качестве примера применения метода 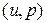 диаграмм задачу, содержащую сильный разрыв в начальных данных (частный случай задачи о распаде произвольного разрыва), для случая плоских волн (
диаграмм задачу, содержащую сильный разрыв в начальных данных (частный случай задачи о распаде произвольного разрыва), для случая плоских волн (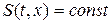 ).
).
З адача. Зададим начальные условия для задачи Коши в виде:
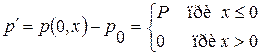 , где
, где  ,
,  .
.
Данные начальные условия моделируют покоящийся газ, разделенный на две части перегородкой (разрывом в начальных данных), в левой части задано возмущение давления 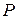 . При
. При  перегородка убирается. Задача найти решение при
перегородка убирается. Задача найти решение при  .
.
Для решения задачи представим в одних осях (на одном графике) 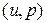 диаграммы для газа, находящегося как слева от перегородки, так и справа (исходные точки
диаграммы для газа, находящегося как слева от перегородки, так и справа (исходные точки 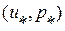 в данном случае будут
в данном случае будут 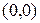 и
и  ).
).

Рис. 1.74
На Рис 1.74 точки обеих сплошных линий, проходящих через т.  , суть множество возможных состояний
, суть множество возможных состояний 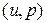 , в которые газ, расположенный слева от перегородки, может перейти, находясь первоначально в состоянии
, в которые газ, расположенный слева от перегородки, может перейти, находясь первоначально в состоянии  , как в результате непрерывного, так и ударного перехода (т. к. кривые
, как в результате непрерывного, так и ударного перехода (т. к. кривые 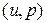 диаграмм для ударных волн и волн разрежения (сжатия) в линейной приближении совпадают). Аналогично точки пунктирных линий, проходящих через т.
диаграмм для ударных волн и волн разрежения (сжатия) в линейной приближении совпадают). Аналогично точки пунктирных линий, проходящих через т. 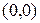 , суть множество возможных состояний
, суть множество возможных состояний 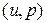 , в которые газ, расположенный справа от перегородки, может перейти, находясь первоначально в состоянии
, в которые газ, расположенный справа от перегородки, может перейти, находясь первоначально в состоянии 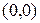 , как в результате непрерывного, так и ударного перехода. Как видно из Рис. 1.74 сплошные и пунктирные линии пересекаются в двух точках А и В. Координаты точки А пересечения прямых, которые находятся по известным уравнениям прямых, суть решение нашей задачи. Точка В, симметричная точке А относительно оси ординат, – решение задачи в случае если расположение газов относительно перегородки поменять местами. Из значений координат точки А
, как в результате непрерывного, так и ударного перехода. Как видно из Рис. 1.74 сплошные и пунктирные линии пересекаются в двух точках А и В. Координаты точки А пересечения прямых, которые находятся по известным уравнениям прямых, суть решение нашей задачи. Точка В, симметричная точке А относительно оси ординат, – решение задачи в случае если расположение газов относительно перегородки поменять местами. Из значений координат точки А 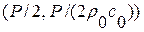 следует, что вправо по покоящемуся газу с пониженным давлением
следует, что вправо по покоящемуся газу с пониженным давлением 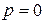 побежит со скоростью
побежит со скоростью  ударная волна сжатия, поднимающая давление в нем на величину
ударная волна сжатия, поднимающая давление в нем на величину 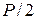 и разгоняющая ранее покоящийся газ до скорости
и разгоняющая ранее покоящийся газ до скорости 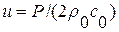 . Соответственно влево по покоящемуся газу с повышенным давлением
. Соответственно влево по покоящемуся газу с повышенным давлением 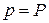 побежит со скоростью
побежит со скоростью  ударная волна разрежения, понижающая давление в нем на величину
ударная волна разрежения, понижающая давление в нем на величину 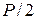 и разгоняющая ранее покоящийся газ до скорости
и разгоняющая ранее покоящийся газ до скорости 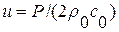 . Ниже представлены эпюры давления и скорости в начальный момент времени и в некоторый момент времени после убирания перегородки (эпюра скорости в начальный момент (
. Ниже представлены эпюры давления и скорости в начальный момент времени и в некоторый момент времени после убирания перегородки (эпюра скорости в начальный момент ( ) не изображена на рисунке).
) не изображена на рисунке).

Чуть позже решение этой задачи будет получено вторым способом, получившим название метода инвариантов Римана.
Инварианты Римана для линеаризованной системы уравнений одномерной газовой динамики для случая плоской симметрии (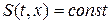 ).
).
Введем новые неизвестные функции  и
и 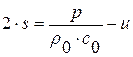 , получившие название инварианты Римана. Тогда условия совместности в системе (1.71)
, получившие название инварианты Римана. Тогда условия совместности в системе (1.71)
перепишутся в виде
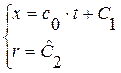 и
и 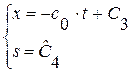 , где
, где  и
и 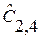 - постоянные (1.73)
- постоянные (1.73)
Вернемся к нашей исходной линеаризованной системе (1.26):
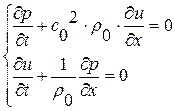
Умножим первое уравнение этой системы на  и сложим со вторым, получим
и сложим со вторым, получим

Теперь из первого вычтем второе, получим
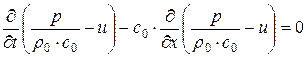
Вспомним определение новых функций  и
и 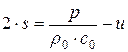 , тогда получим для r и s систему
, тогда получим для r и s систему
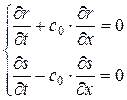 (1.74)
(1.74)
Характеристики первого уравнения - семейство  , т. е.
, т. е.  , общее решение уравнения
, общее решение уравнения 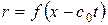 ; для второго уравнения характеристики – семейство
; для второго уравнения характеристики – семейство 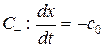 , т. е.
, т. е.  , общее решение
, общее решение 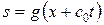 , где f и g любые дифференцируемые функции. Зная r и s, найдем
, где f и g любые дифференцируемые функции. Зная r и s, найдем  и u.
и u.
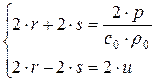
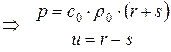
Как уже отмечалось, функции r и s называются инвариантами Римана. Вдоль каждой характеристики неизменны вдоль  — инвариант r, вдоль
— инвариант r, вдоль  — инвариант s.
— инвариант s.
При 
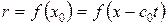 ,
, 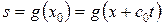 . Эти формулы также как и формулы (1.72) показывают, что
. Эти формулы также как и формулы (1.72) показывают, что

т. к. вдоль 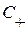 имеем
имеем 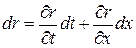 , где
, где  или
или 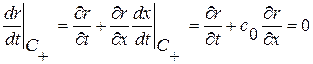 ; Аналогично
; Аналогично  .
.
Итак, постоянное значение r распространяется вправо со скоростью 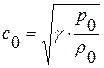 , постоянное значение s распространяется влево со скоростью
, постоянное значение s распространяется влево со скоростью 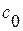 . Величину
. Величину 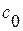 называют скоростью распространения звуковой волны или, сокращенно, скоростью звука.
называют скоростью распространения звуковой волны или, сокращенно, скоростью звука.
В нашем линейном случае все характеристики 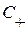 параллельны, поэтому все возмущения r идут с одной и той же скоростью
параллельны, поэтому все возмущения r идут с одной и той же скоростью 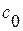 , т. е. возмущения для r идут без искажения. Аналогично для
, т. е. возмущения для r идут без искажения. Аналогично для 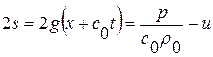 постоянные значения s идут по
постоянные значения s идут по  - характеристикам со скоростью
- характеристикам со скоростью 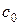 влево без искажения. Зная r и s, получим
влево без искажения. Зная r и s, получим
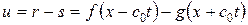 (1.75)
(1.75)
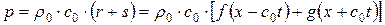 (1.76)
(1.76)
 Конечно, по известному значению давления (1.76) можно найти и плотность
Конечно, по известному значению давления (1.76) можно найти и плотность 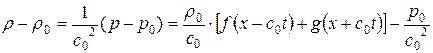
Рис. 2.6
На Рис. 2.6 изображен характеристический треугольник 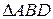 и характеристики обоих семейств.
и характеристики обоих семейств.
Попробуем теперь определить функции f и g таким образом, чтобы полученное решение (1.75), (1.76) удовлетворяло условиям задачи Коши при задании начальных значений 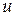 и
и  на отрезке AB (или на всей оси Ox).
на отрезке AB (или на всей оси Ox).
Решение задачи Коши для линейной системы (1.26) при помощи инвариантов Римана.
Дата добавления: 2015-10-23; просмотров: 128 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Характеристики – линии распространения разрывов производных решений интегрального аналога (1.56) волнового уравнения (линии слабого разрыва). | | | Начальные данные (при ). |