Общее решение волнового уравнения для случая плоских волн.

Рассмотрим вначале случай плоских () волн. Тогда волновое уравнение (1.29.2) примет вид: , (1.30.0)

Введем новые независимые переменные, получившие название характеристических переменных, , . (1.30.1)

Заметим, что якобиан преобразования (1.30.1) не вырожден для любых значений 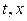и равен по величине .

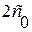Тогда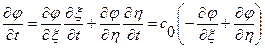

Вторая производная

.

Аналогично

. Подставляя в (1.30.0) найденные значения вторых производных получим

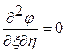, т. е. или 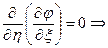интегрируя по 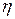, получим .

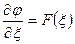Проинтегрируем получившееся уравнение по 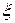, получим

.

Возвращаясь к старым переменным, получим , (1.30.2) где 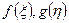- произвольные дважды непрерывно дифференцируемые функции.

Это решение было получено Ж. Д’ Аламбером в 1747 г. и является комбинацией (наложением) прямой и обратной волн: одна волна неизменной формы, описываемой функцией 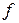, движется вправо со скоростью , а другая с формой, описываемой функцией 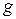, движется влево с такой же скоростью . Действительно, полагая в найденных решениях 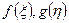значения их аргументов равными константе 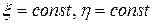, получим две системы плоских волн:

, (1.30.3)

представляющих две движущиеся в противоположные стороны со скоростью перпендикулярные оси 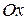плоскости, каждая из которых несет постоянные, заданные начальными условиями значения возмущений скорости, давления, плотности или температуры. С геометрической точки зрения полученное решение можно интерпретировать как наличие в фазовой плоскости двух семейств прямых (1.30.3) с угловыми коэффициентами 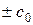, обладающих тем свойством, что вдоль каждой их этих прямых сохраняются постоянные значения заданных начальными условиями возмущений скорости, давления, плотности или температуры. Эти два семейства прямых называются характеристиками волнового уравнения (1.30.0) в фазовой плоскости.

Рис. 1.2

Заметим, что процедура нахождения решения волнового уравнения была бы значительно проще в случае только одной волны. Нужное для этого уравнение получается факторизацией (разложением) волнового уравнения (1.30.0)

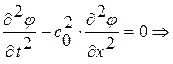
(1.31.0)

и оставлением только одного из сомножителей. Оставив, например,

(1.31.1)

получим общее решение уравнения (1.31.1) в виде

(1.31.2)

Примечание: Рассмотрим обыкновенное дифференциальное уравнение 1-ого порядка относительно функции 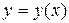, записанное в виде

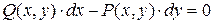(1.32.1)

Оно равносильно уравнению в частных производных первого порядка

(1.32.2)

в том смысле, что левая часть всякого интеграла 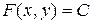, где 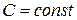, уравнения (1.32.1) является решением уравнения (1.32.2), и обратно, всякое решение 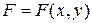уравнения (1.32.2), приравненное произвольной постоянной, дает интеграл уравнения (1.32.1).

Действительно: 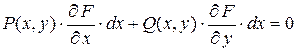то, с учетом (1.32.1), имеем

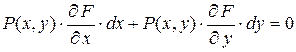, след., 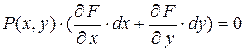, т. е. для имеем 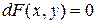, след., 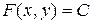, где .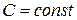

Воспользовавшись примечанием, найдем сопряженное обыкновенное дифференциальное уравнение к исходному уравнению (1.31.1): , имеющее первый интеграл вида 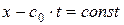, более того, любая непрерывно дифференцируемая функция 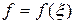, где , дает наиболее общий вид первого интеграла 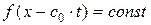. cопряженного о/д/у. Поэтому, (1.31.2) - общее решение (1.31.1), которое можно было получить и другим способом - через указанную выше замену переменных .

Укажем еще один способ построения общего решения волнового уравнения, основанный на разложении оператора (1.31.0). Благодаря разложению (1.31.0) волновое уравнение сводится к двум последовательно решаемым уравнениям в частных производных первого порядка, т. е. уравнение 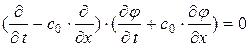равносильно двум последовательно сцепленным уравнениям 1. 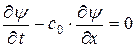и 2. 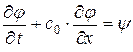. Решение однородного уравнения 1. нам известно 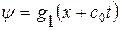. Тогда уравнение 2. примет вид 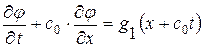, общее решение которого будем искать как сумму общего решения однородного уравнения плюс частное решение неоднородного уравнения():

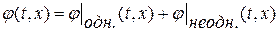общее решение однородного уравнения 2. известно , частное решение неоднородного 2. будем искать, исходя из вида правой части уравнения, в виде 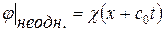. Тогда уравнение 2. примет вид или 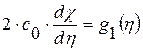, след., , где . Интеграл от произвольной функции дает произвольную дифференцируемую функцию, умножение на константу не выводит за пределы этого класса. Таким образом, общее решение неоднородного уравнения примет вид 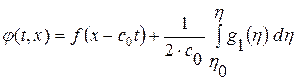. Обозначим 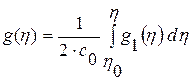и, заменив 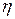на его значение 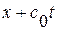, вновь получим ранее найденное путем замены переменных общее решение волнового уравнения .

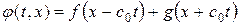Получим теперь соответствующие найденному общему решению выражения для возмущений скорости и давления:

,

,

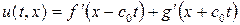где обозначает обыкновенную производную 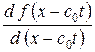функции 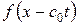по аргументу и аналогично для функции .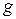

Обозначим .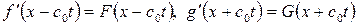

Тогда в новых обозначениях

,

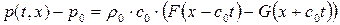где 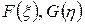- произвольные один раз непрерывно дифференцируемые функции.

Полученные выражения для возмущений скорости и давления – суть общее решение системы уравнений (1.26) для плоского случая .

Дата добавления: 2015-10-23