
Читайте также:
|
Найденная функция  (1.35)
(1.35)
представляет процесс распространения начального профиля и начальной скорости возмущения. Если фиксировать  , то функция
, то функция  дает профиль возмущения в момент
дает профиль возмущения в момент  ; фиксируя
; фиксируя  , получим функцию
, получим функцию  , дающую процесс движения точки
, дающую процесс движения точки  . Предположим, что наблюдатель, находившийся в точке
. Предположим, что наблюдатель, находившийся в точке  в момент
в момент  , движется со скоростью
, движется со скоростью  в положительном направлении. Введем систему координат, связанную с наблюдателем, полагая
в положительном направлении. Введем систему координат, связанную с наблюдателем, полагая  . В этой подвижной системе отсчета функция
. В этой подвижной системе отсчета функция  будет определяться формулой
будет определяться формулой  и наблюдатель все время будет видеть тот же профиль, что и в начальный момент. Следовательно, функция
и наблюдатель все время будет видеть тот же профиль, что и в начальный момент. Следовательно, функция  представляет неизменный профиль
представляет неизменный профиль  , перемещающийся вправо по оси
, перемещающийся вправо по оси 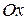 со скоростью
со скоростью  (т. е. бегущую с постоянной скоростью вправо волну неизменной формы). Функция
(т. е. бегущую с постоянной скоростью вправо волну неизменной формы). Функция  представляет, очевидно, волну, распространяющуюся влево со скоростью
представляет, очевидно, волну, распространяющуюся влево со скоростью  . Т. о., общее решение (1.35) задачи Коши для бесконечного промежутка
. Т. о., общее решение (1.35) задачи Коши для бесконечного промежутка  есть суперпозиция двух волн
есть суперпозиция двух волн  , одна из которых распространяется вправо со скоростью
, одна из которых распространяется вправо со скоростью  , а вторая - влево с той же скоростью. При этом
, а вторая - влево с той же скоростью. При этом

где  .
.
Для выяснения характера решения (1.35) удобно воспользоваться фазовой плоскостью  . Прямые
. Прямые  в фазовой плоскости называются характеристиками волнового уравнения. Функции
в фазовой плоскости называются характеристиками волнового уравнения. Функции  сохраняет постоянное значение вдоль характеристики
сохраняет постоянное значение вдоль характеристики  , а функция
, а функция  постоянна вдоль характеристики
постоянна вдоль характеристики  .
.
 Предположим теперь, что функция
Предположим теперь, что функция  отлична от нуля только в интервале
отлична от нуля только в интервале  и равна нулю вне этого интервала. Проведем характеристики семейства
и равна нулю вне этого интервала. Проведем характеристики семейства  через концы интервала
через концы интервала  и
и 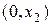 ; они разбивают полуплоскость
; они разбивают полуплоскость  на три области: I, II, II (Рис. 1.3).
на три области: I, II, II (Рис. 1.3).
Рис. 1.3
Функция  отлична от нуля только в обл. II, где
отлична от нуля только в обл. II, где  , а характеристики
, а характеристики  представляют собой задний и передний фронты распространяющейся вправо волны.
представляют собой задний и передний фронты распространяющейся вправо волны.
Рассмотрим теперь некоторую фиксированную точку  и проведем из нее обе характеристики
и проведем из нее обе характеристики 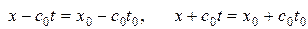 , которые пересекут ось
, которые пересекут ось 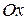 в точках
в точках  . Значение функции
. Значение функции 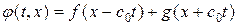 в точке
в точке  равно
равно  , т. е. определяется значениями функций
, т. е. определяется значениями функций  и
и  в точках
в точках  и
и  , являющихся вершинами треугольника MPQ, образованного двумя характеристиками и осью
, являющихся вершинами треугольника MPQ, образованного двумя характеристиками и осью 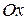 (Рис. 1.4).
(Рис. 1.4).

 Рис. 1.4
Рис. 1.4
Этот треугольник MPQ называется характеристическим треугольником точки  .
.
Из формулы (1.35) видно, что величина амплитуды 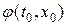 в точке М в момент времени
в точке М в момент времени  зависит только от значений начального возмущения в вершинах Р и Q характеристи-ческого треугольника MPQ и от значений начальной скорости на стороне PQ. Это становится совершенно ясно, если формулу (1.35) записать в виде:
зависит только от значений начального возмущения в вершинах Р и Q характеристи-ческого треугольника MPQ и от значений начальной скорости на стороне PQ. Это становится совершенно ясно, если формулу (1.35) записать в виде:

Начальные данные, заданные вне PQ, не оказывают влияния на значение 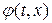 в точке М. Заметим, что, если начальные данные заданы не на всей бесконечной прямой
в точке М. Заметим, что, если начальные данные заданы не на всей бесконечной прямой 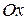 , а на некотором отрезке
, а на некотором отрезке  , то они однозначно определяют решение внутри характеристического треугольника, основанием которого является отрезок
, то они однозначно определяют решение внутри характеристического треугольника, основанием которого является отрезок  .
.
Перепишем также формулы (1.34.7) для значений возмущения скорости и давления:


Видно, что значения возмущений скорости и давления в точке М зависят только от начальных данных в точках P и Q.
Два примера: Решение задачи Коши для волнового уравнения (1.35) можно также представить в виде в суммы функций:
 , (1.36)
, (1.36)
где  , (1.37)
, (1.37)
где  , (1.38)
, (1.38)
тогда, если начальная скорость возмущения равна нулю ( ), то амплитуда возмущения
), то амплитуда возмущения  есть сумма левой и правой бегущих волн, причем начальная форма каждой волны определяется функцией
есть сумма левой и правой бегущих волн, причем начальная форма каждой волны определяется функцией  , равной половине начального возмущения. Если же наоборот
, равной половине начального возмущения. Если же наоборот  и
и  , то решение
, то решение  представляет возмущение, создаваемое начальной скоростью.
представляет возмущение, создаваемое начальной скоростью.
Пример 1: Рассмотрим распространение начального возмущения  и
и  , заданного на отрезке
, заданного на отрезке  , при помощи представления решения в виде (1.36). Для этого проведем характеристики обоих семейств через точки
, при помощи представления решения в виде (1.36). Для этого проведем характеристики обоих семейств через точки  и
и 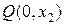 ; они разобьют верхнюю полуплоскость на шесть областей (Рис. 1.5). Величина возмущения для наших начальных данных дается формулой (1.37), т. е.
; они разобьют верхнюю полуплоскость на шесть областей (Рис. 1.5). Величина возмущения для наших начальных данных дается формулой (1.37), т. е.  в любой точке
в любой точке  . Поэтому в областях I, III, V возмущение равно нулю, т. к. боковые стороны характеристического треугольника для любой точки из этих областей не пересекаются с отрезком PQ, на котором задано начальное возмущение. В области II решением является правая волна
. Поэтому в областях I, III, V возмущение равно нулю, т. к. боковые стороны характеристического треугольника для любой точки из этих областей не пересекаются с отрезком PQ, на котором задано начальное возмущение. В области II решением является правая волна

Рис. 1.5
 , в области IV – левая волна
, в области IV – левая волна  , а в области VI решение есть сумма левой и правой волн. Область, образованная областями II+IV+VI, называется областью влияния начальных данных, заданных на отрезке PQ. (Схематически для случая начального возмущения в форме треугольника последовательные положения профиля волны представлены на Рис. 1.6.1)
, а в области VI решение есть сумма левой и правой волн. Область, образованная областями II+IV+VI, называется областью влияния начальных данных, заданных на отрезке PQ. (Схематически для случая начального возмущения в форме треугольника последовательные положения профиля волны представлены на Рис. 1.6.1)
 В случае задания на отрезке PQ ненулевого значения начальной скорости возмущения (т.е.
В случае задания на отрезке PQ ненулевого значения начальной скорости возмущения (т.е.  ) область влияния включала бы в себя области II+IV+VI и плюс область III.
) область влияния включала бы в себя области II+IV+VI и плюс область III.
Рис. 1.6.1
Пример 2: Рассмотрим распространение возмущения со следующими начальными данными: начальное возмущение отсутствует ( ), а начальная скорость
), а начальная скорость 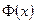 отлична от нуля только на отрезке
отлична от нуля только на отрезке  , где она принимает постоянное значение
, где она принимает постоянное значение 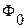 :
:
 при
при 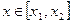 ,
,  при
при  и
и  . В этом случае решением является функция
. В этом случае решением является функция  из (1.36)-(1.38). Вычислим функцию
из (1.36)-(1.38). Вычислим функцию  , положив при этом
, положив при этом  (график функции дан на Рис. 1.6.2):
(график функции дан на Рис. 1.6.2):

Решение  есть разность правой и левой волн с профилем
есть разность правой и левой волн с профилем  . Последовательные положения этих волн в моменты времени
. Последовательные положения этих волн в моменты времени  изображены на Рис. 1.6.3. Изначально нулевой профиль возмущения с ростом времени
изображены на Рис. 1.6.3. Изначально нулевой профиль возмущения с ростом времени  приобретает форму трапеции, расширяющейся равномерно с течением времени. Заметим, что, если
приобретает форму трапеции, расширяющейся равномерно с течением времени. Заметим, что, если 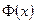 отлична от постоянной на отрезке
отлична от постоянной на отрезке  , то изменится только профиль
, то изменится только профиль  .
.
Для выяснения характера полученного решения воспользуемся фазовой плоскостью 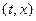 .
.
Напишем выражения для  в различн. областях фазовой пл-ти (Рис. 1.5).
в различн. областях фазовой пл-ти (Рис. 1.5).
В обл. I. (  ):
): 
В обл. V. (  ):
): 
В обл. III. (  ):
): 
В обл. II. (  ):
): 
В обл. IV. (  ):
): 
В обл. VI. (  ):
): 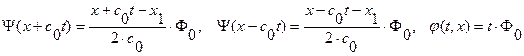

Понятие устойчивости решения.
Найденное нами решение Д’ Аламбера (1.35) задачи Коши для волнового уравнения (1.34.1) однозначно определено начальными условиями (1.34.2). Докажем теперь, что это решение меняется непрерывно при непрерывном изменении начальных условий.
Утверждение: Каков бы ни был промежуток времени 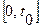 и какова бы ни была степень точности
и какова бы ни была степень точности 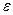 , найдется такое
, найдется такое  , что всякие два решения волнового уравнения (1.34.1)
, что всякие два решения волнового уравнения (1.34.1) 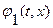 и
и  в течение промежутка времени
в течение промежутка времени  будут различаться меньше чем на
будут различаться меньше чем на 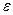 :
:
 ,
,
если только начальные значения
 и
и 
отличаются друг от друга меньше, чем на  :
:
 .
.
Доказательство:
Функции 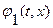 и
и  связаны со своими начальными значениями формулой Д’Аламбера (1.35), поэтому справедлива оценка
связаны со своими начальными значениями формулой Д’Аламбера (1.35), поэтому справедлива оценка

из этой оценки получаем
 , и далее выбор
, и далее выбор  доказывает наше утверждение.
доказывает наше утверждение.
Если решение математической задачи непрерывно зависит от дополнительных условий (от начальных, граничных данных и от правой части уравнения – т. е. от исходных данных задачи), то говорят, что задача устойчива.
Говорят, что математическая задача поставлена корректно, если:
Отметим одно важное обстоятельство. Очевидно, что функция 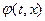 , определяемая формулой (1.35), может быть решением волнового уравнения только в том случае, если функция
, определяемая формулой (1.35), может быть решением волнового уравнения только в том случае, если функция 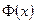 дифференцируема, а функция
дифференцируема, а функция  дифференцируема дважды. Из сказанного ясно, что функции, изображенные на Рис. 1.6, не могут являться решением волнового уравнения, т.к. они не всюду дважды дифференцируемы. Однако если немного изменить начальные условия (сгладить), заменив их дифференцируемыми функциями
дифференцируема дважды. Из сказанного ясно, что функции, изображенные на Рис. 1.6, не могут являться решением волнового уравнения, т.к. они не всюду дважды дифференцируемы. Однако если немного изменить начальные условия (сгладить), заменив их дифференцируемыми функциями  и
и 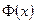 , то этим начальным функциям уже будет соответствовать решение волнового уравнения (1.34.1). Кроме того заметим, что при доказательстве утверждения настоящего пункта мы фактически доказали, что функции, определяемые формулой (1.35), непрерывно зависят от начальных функций
, то этим начальным функциям уже будет соответствовать решение волнового уравнения (1.34.1). Кроме того заметим, что при доказательстве утверждения настоящего пункта мы фактически доказали, что функции, определяемые формулой (1.35), непрерывно зависят от начальных функций  и
и 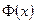 (независимо от того, дифференцируемы эти функции или нет). Т. о., если некоторым функциям
(независимо от того, дифференцируемы эти функции или нет). Т. о., если некоторым функциям  и
и 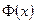 не соответствует решение волнового уравнения, удовл. нач. усл. (1.34.2), то функция, определяемая формулой (1.35), является пределом решений волнового уравнения с немного сглаженными начальными условиями. Полученные таким предельным переходом функции называются обобщенными решениями, понятие которых было введено С.Л. Соболевым.
не соответствует решение волнового уравнения, удовл. нач. усл. (1.34.2), то функция, определяемая формулой (1.35), является пределом решений волнового уравнения с немного сглаженными начальными условиями. Полученные таким предельным переходом функции называются обобщенными решениями, понятие которых было введено С.Л. Соболевым.
Дата добавления: 2015-10-23; просмотров: 135 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задача Коши для волнового уравнения в случае плоских волн. | | | Задача Коши для волнового уравнения на полуограниченной прямой. Метод продолжений. |