Обчислення похибки при непрямих вимірюваннях величин

Досить часто трапляється ситуація, коли безпосередньо поміряти значення певної величини неможливо. Проте, знаючи модельну залежність цієї величини

від інших величин (формулу), значення її можна розрахувати. Таке вимірювання називається непрямим.

Наприклад, щоб визначити площу S, ми міряємо його радіус R і обчислюємо площу за формулою:

(2.1)

Як, знаючи точність вимірювання R, оцінити значення похибки S? Точність непрямих вимірювань залежить як від способу вимірювання (формули), так і від точності вимірів усіх величин, які в цю формулу входять.

К.Ф.Гаусс, вважаючи похибку вимірів малою, запропонував лінеаризувати вираз для обчислення результату в околі середніх значень поміряних величин і шукати похибку так, як знаходять повний диференціал функції. Єдина відмінність полягає у використанні того факту, що похибки — завжди додатні величини.

Покажемо підхід Гауса на прикладі функції:

. (2.2)

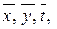Лінеаризуючи в околі значень отримаємо вираз для обчислення повного диференціала:

(2.3)

Значення часткових похідних, взятих по модулю,

(2.4)

в теорії похибок називають чутливостями функції відповідно до змін величин .

Для визначення абсолютної похибки непрямого вимірювання користуються формулою:

(2.5)

тобто, похибку непрямого вимірювання шукають згідно з тими ж правилами, що й повний диференціал цієї величини. Формальна відмінність полягає в тому, що всі арифметичні знаки ± при чутливостях змінюються на знаки +, а знаки диференціалів d – на значки похибок Δ.

Наведемо формули для обчислення абсолютних і відносних похибок:

1) суми:

, (2.6)

2) різниці:

(2.7)

3) добутку:

(2.8)

4) степеня:

;(2.9)

5) дробу:

(3.0)

6) кореня:

(3.1)

Якщо вираз для шуканої величини не містить значків ”+”чи “-“ (є термом), зручніше спочатку знаходити відносну похибку відповідно до правила: відносна похибка результату дорівнює сумі відносних похибок окремих змінних, взятих із такими коефіцієнтами, в якому степені вони входять у терм.

Наприклад, якщо шукана величина задана виразом:

,

то відносна похибка визначатиметься співвідношенням:

.

Дата добавления: 2015-10-23