Расчет трубопроводов для газов

Продукты, участвующие в процессе разделения, могут находиться как жидкой, так в газовой фазах, поэтому рассмотрим особенности расчета трубопроводов, используемых для транспортировки газов.

Под углом зрения гидравлических расчетов различают два случая течения газа: течение при малых относительных перепадах давления и течение при больших перепадах (имеется в виду перепад Δ p между начальным и конечным сечениями труб, отнесенный к среднему давлению). В первом случае, возможно, пренебрегать сжимаемостью газов, т. е. считать объемный вес транспортируемого газа неизменным по всей длине трубопровода; тогда расчеты газопроводов принципиа­льно не отличаются от расчетов для несжимаемых жидкостей. При больших относительных перепадах (примерно, если Δ p / p > 5%) прене­брегать сжимаемостью газа нельзя и нужно учитывать непрерывный характер изменения объемного веса газа в зависимости от давления.

Течение газа при малых перепадах давления. При расчете тече­ния газа в трубах обычно рассматривают потери не напора, а давления.

Формулы для определения потерь на трение и местных потерь в этом случае примут вид

, (7.31)

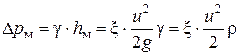, (7.32)

здесь D р – потерянное давление; g – средний объемный вес газа

,

где р ₁ и р ₂ – значения давления в концевых сечениях трубопровода.

Тогда уравнение Бернулли при расчете трубопроводов для газов при малых перепадах давления запишется в виде

. (7.33)

Если трубы имеют некруговое сечение, то вместо диаметра вводится эквивалентный диаметр.

При расчетах вентиляции потери на местные сопротивления имеют, как правило, большую величину, чем потери на трение.

В длинных газопроводах, наоборот, потери давления на местные сопротивления невелики по сравнению с потерями давления на трение, и здесь можно полагать

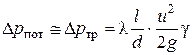. (7.34)

Коэффициент гидравлического трения l, входящий в эту формулу, определяется по тем же формулам, что и при движении несжимаемых жидкостей по трубам.

Расчет газопровода при больших перепадах давления. В этом случае нельзя без больших погрешностей полагать объемный вес газа постоянным по длине трубопровода, как это делается при расчете газо­проводов низкого давления; кроме того, даже при сохранении постоян­ства диаметра по длине газопровода движение газа в таких трубопро­водах является неравномерным. Действительно, в соответствии с урав­нением неразрывности

ρ Su = const

или при S = const, ρ u = const

Но давление газа по длине газопровода уменьшается, т. е. умень­шается его плотность, следовательно, возрастает скорость течения газа, которая в конце газопровода всегда выше, чем в его начале.

При расчетах таких газопроводов можно пренебрегать не только изменениями удельной энергии положения в уравнении Бернулли, но также изменениями удельной кинетической энергии газа.

Поэтому при расчетах движения газов с большими перепадами давления уравнение Бернулли сводится к зависимости (для бесконечно малого участка трубопровода, на котором объемный вес газа и скорость его течения можно считать постоянными)

. (7.35)

С учетом формулы Дарси-Вейсбаха формула (7.35) получает вид

. (7.36)

Для интегрирования этого уравнения нужно знать зависимости g = f (l), u = f ₁(l) и l = f ₂(l).

Эти зависимости определяются термодинамическими процессами, имеющими место при движении газа по трубопроводу.

Для коэффициента гидравлического трения λ, как известно, имеет место зависимость

.

Относительная шероховатость по длине газопровода не меняется. Число Рейнольдса можно выразить через весовой расход G в виде

Re = r ud /m = 4 G /(g mp d).

При изотермическом течении динамический коэффициент вязкости m остается постоянным по длине трубопровода, следовательно, неизмен­но и число Рейнольдса. Таким образом, несмотря на изменение средней скорости течения газа и его объемного веса, величина коэффициента гидравлического трения вдоль газопровода не меняется. Скорость u и плотность r в любом сечении газопровода связаны со скоростью и плотностью в начальном сечении u ₁ и r₁ уравнением неразрывности:

u = u ₁r₁/r.

Подставляя это выражение в (7.36), получим

. (7.37)

С другой стороны из уравнения состояния газа

r = p /(gRT), (7.38)

имеем

,

в соответствии с чем (7.37) можно привести к виду

.

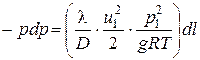Интегрируя это уравнение от р ₁ до р ₂, получим

.

Тогда, используя (7.38), имеем

. (7.39)

С учетом формулы (7.39), для участка газопровода длиной L, давле­ния в начале участка – p _н и в конце – p _к , можно связать соотношением:

а распределение давления p (l) на этом участке, представить в виде

p ²(l) = p _н² – (p _н² – p _к²) l / L. (7.39а)

Уравнение (7.39) можно переписать также в виде

. (7.39б)

Левая часть последнего уравнения может быть преобразована к виду

,

поэтому (7.39б) примет вид

.

Но p ₂/ p ₁ = (p ₁ – D p)/ p ₁ = 1 – D p / p ₁,

следовательно, окончательно получим

. (7.39в)

Уравнение (7.39в) отличается от формулы Дарси–Вейсбаха для определения потерь давления при движении несжимаемой жидкости лишь множителем, зависящим от величины отношения Δ p / p ₁. До тех пор, пока сохраняется условие Δ p / p ₁ < 5 %, пренебрежение этим мно­жителем дает ошибку около 2,5%, что допустимо в большинстве инженерных расчетов.

Формула для определения расхода газа имеет вид

. (7.40)

Коэффициент l, входящий в эту формулу, определяется по тем же формулам, что и при движении несжимаемых жидкостей по трубам.

Дата добавления: 2015-10-29