Потери напора в арматуре трубопроводов, в тройниках и крестовинах

Потери напора в арматуре трубопроводов. В трубопроводах в ряде случаев приходится ставить различные приспособления для искусственного создания сопротивления: задвижки, клапаны, затворы и пр. В этих устройствах имеет место сужение потока с его последующим расширением, а также иногда и повороты.

С гидравлической точки зрения подобные устройства действуют аналогично диафрагме, и поэтому в первом приближении коэффициент местного сопротивления в этих случаях может быть найден по формуле (6.17). В таблице 6.4 приведены значения x, подсчитанные по формуле (6.17) при разных п. Эти значения вполне удовлетворительно согласуются с опытными данными для запорных устройств типа задвижек. Таким образом, можно прийти к выводу, что местное сопротивление подобных запорных устройств зависит главным образом от степени их прикрывания и меньше от конструкции.

Потери напора в дросселе (рис. 6.11) и кране (рис. 6.12) зависят от угла поворота d. При d = 0° сопротивление как дросселя, так и крана будет наименьшим. С увеличением d потери возрастают, и при d = 90° коэффициент сопротивления становится бесконечно большим. Числен­ные значения коэффициента x для дросселя и крана, установленных в круглой трубе, приведены в таблице 6.5.

Как правило, коэффициенты местных сопротивлений арматуры можно найти из таблиц, составленных на основании опытных данных.

Таблица 6.4

Значения коэффициента местного сопротивления для диафрагмы и запорных устройств на трубопроводах

n	0,1	0,2	0,3	0,4	0,5	0,6
x по формуле (6.17)		50,3	19,9	9,8	4,4	2,4

Таблица 6.5

Численные значения коэффициента местного сопротивления для дросселя и крана, установленных в круглой трубе

Угол d
x дросселя	0,24	0,52	1,54	3,91	10,8	32,6
x крана	0,05	0,29	1,56	5,47	17,3	52,6			–

Потери напора в стыках. Важным вопросом гидравлического расчета трубопроводов является учет потерь напора, вызываемых стыками. Последние можно рассматривать как местные сопротивления, естественно, что с уменьшением диаметра трубы влияние стыков на сопротивление увеличивается.

Сопротивления, вызванные стыками, можно найти по формуле

K = 1+ (x_ст/l)·(d/l), (6.41)

где K = l₁/l – относительное увеличение сопротивления трубопровода (отношение сопротивления трубопровода со стыками к сопротивлению трубопровода без стыков); l – расстояние между стыками (длина труб); d – диаметр труб; l – коэффициент гидравлического трения трубопро­вода без стыков.

Значение коэффициента x_ст в этой формуле можно принимать в зависимости от технологии сварки по таблице 6.6.

Потери напора в тройниках и крестовинах. Тройником называется деталь трубопровода, в которой происходит слияние или разделение потока. Тройники делятся на приточные (нагнетательные), когда жидкость из магистрали течет в ответвление (рис. 6.13), и вытяжные (всасывающие), когда жидкость поступает из ответвления в магистраль (рис. 6.14). Потери напора в тройниках возникают в резуль­тате отрыва потока от стенки с последующим расширением.

Таблица 6.6

Значения коэффициента x_ст для различных видов сварных стыков

Вид стыка	Диаметр труб d, мм
С подкладными кольцами d = 5 мм	0,06	0,03	0,018	0,013	0,009	0,007	0,006
Электродуговые и контактные	0,026	0,014	0,009	0,006	0,004	0,003	0,002

Введем следующие обозначения: m – массовый расход жидкости в трубе; d – диаметр трубы; u – скорость течения в ней; эти величины, относящиеся к боковому ответвлению, прямому проходу и сборному рукаву тройника, будем обозначать индексами б, п, и с, соответствен­но; через d обозначим угол ответвления. Потери напора у потоков, идущих из бокового ответвления или обратно h _с.б и прямого прохода тройника h _с.п, будем относить к скорости потока в сборном рукаве тройника и записывать их в виде

h _с.б = x_с.б u _с²/(2 g), h _с.п = x_с.п u _с²/(2 g).

где x_с.б и x_с.п – коэффициенты сопротивления бокового ответвления и прямого прохода тройника, приведенные к скорости в сборном рукаве тройника.

Величина x_с.б и x_с.п зависит от угла d, от соотношений площадей сечений ответвлений (боковых и прямого), от соотношения расходов жидкости в ответвлениях, а также от направления течения.

Несмотря на наличие ряда работ, посвященных расчету течения в тройниках, этот вопрос с теоретической точки зрения изучен еще недо­статочно. Поэтому, обычно коэффициенты местных сопротивлений различного вида тройников находят по полуэмпирическим формулам, таблицам и графикам, полученных на основе экспериментов.

Так для вытяжного тройника (рис. 6.14), в наиболее простом и часто встречающемся на практике случае (d _с = d _п; d = 90°), величины коэффициентов сопротивления прохода x_с.п и бокового ответвления x_с.б можно найти по формулам

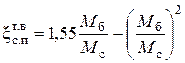, (6.42)

, (6.43)

где индекс т. в – тройник вытяжной; А – некоторый коэффициент, значение которого можно найти по таблице 6.7.

Таблица 6.7

Значение коэффициента А

S б/ S с	£ 0,35	> 0,35
m б/ m с	£ 1,0	£ 0,4	> 0,4
A	1,0	0,9(1 – m б/ m с)	0,55

Например, при S _с = S _б, и m _б/ m _с = 0,1, значение коэффициента боко­вого ответвления , рассчитанное по формуле (6.43), равно

.

т. е. коэффициент сопротивления получается отрицательным, что озна­чает увеличение энергии жидкости в соответствующем направлении течения. Действительно, при m _б = 0,1 m _с скорость течения u _п > u _c; поэтому при слиянии струя прямого прохода (первая) увлекает за собой трением струю из ответвления (вторую) и передает ей часть своей энергии. В результате первая струя имеет большие потери на­пора, в то время как вторая не только их не имеет, но даже приобретает некоторый напор, и коэффициент x у нее становится отрицательным. С возрастанием величины отношения m _б/ m _с коэффициент сопротивления увеличивается и приобретает постепенно положительное значение.

При изменении направления течения в боковом ответвлении, т. е. в случае, когда тройник является приточным (рис. 6.13), при d _с = d _п и d = 90°, величины коэффициентов сопротивления бокового ответвле­ния x_с.б и прохода x_с.п определяются по формулам

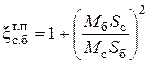, (6.44)

, (6.45)

где индекс т. п – тройник приточный; t_п – некоторый коэффициент, значение которого можно найти по таблице 6.8.

И еще один, часто встречающемся в практике тройник – это трой­ник симметричной формы (равносторонний) с резким углом поворота на 90° (рис. 6.15), который также может работать в режимах слияния и разделения потоков. Формулы для расчета коэффициента сопротивле­ния бокового ответвления в симметричном тройнике при слиянии и разделении потоков, соответственно, имеют вид:

Таблица 6.8

Значение коэффициента t_п

S б/ S с	£ 0,4	> 0,4
m б/ m с	£ 1,0	£ 0,5	> 0,5
tп	0,4	2(2 m б/ m с – 1)	0,3(2 m б/ m с – 1)

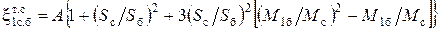, (6.46)

. (6.47)

Для другого бокового ответвления вместо индекса 1 применяется индекс 2. Коэффициент А находится по таблице 6.7.

Крестовины (рис. 6.16), как и тройники, подразделяются на вытяжные, когда в них происходит слияние потоков, и приточные, когда потоки в них разделяются.

Характер потока в крестовинах в основном аналогичен потоку в тройниках. Так коэффициенты сопротивления крестовин при делении потока (приточные крестовины) определяются ориентировочно как для приточных тройников, т. е. по формулам (6.44) и (6.45).

Информацию для расчета потерь в других, нерассмотренных в этом параграфе, видах соединительных устройств и арматуры можно найти в специализированных справочниках по гидравлическим сопротивле­ниям, например [12].

* * *

Таким образом, в § 6:

– Рассмотрены такие понятия, как степень сжатия и расширения пото­ка, коэффициент сжатия струи, конфузор, диффузор и тройник.

– Приведены формулы расчета местных потерь напора в случае внезап­ного расширения (формула Борда), сужения, а также постепенного расширения и сужения потока. Даны выражения Жуковского и Альтшуля для расчета коэффициента сжатия струи.

– Рассмотрены особенности расчета потерь напора при изменении направления потока, т.е. в различного рода коленах, отводах.

– Приведены выражения для расчета потерь напора в арматуре (дрос­селях и кранах) трубопровода, на стыках труб, а также в тройниках и крестовинах.

Вопросы и задачи

1. Сформулируйте понятие эквивалентной длины. Приведите выражение, связы­вающее ее с коэффициентами сопротивлений. Какие группы местных потерь Вы знаете?

2. Раскройте понятия коэффициента сжатия струи, степени сжатия и расширения потока, конфузора и диффузора. Приведите выражение для приближенного определения степени сжатия струи.

3. Напишите формулы для расчета потерь напора при внезапном расширении и сужении потока. Как изменятся эти формулы, если расширение и сужение потока будет постепенным.

4. Чем обусловлены потери напора при изменении направления потока? Приведите формулу для определения коэффициент местного сопротивления колена.

5. Как с гидравлической точки зрения действуют краны, клапаны, дроссели? Напишите формулу для оценки местного сопротивления, вызванного стыками.

6. Сформулируйте понятие тройника. Чем отличаются приточные и вытяжные тройники и крестовины? Какие параметры влияют на величину коэффициентов местных сопротивлений тройников и крестовин?

Задача 1. В качестве нагревательных приборов системы отопления цеха использованы стальные трубы d ₁ = 100 мм. Стояк, подводящий нагретую воду, и соединительные линии, выполнены из труб d ₂ = 25 мм и приварены к торцу труб d ₁. Определить потери давления при внезапном расширении трубопроводов, если скорость движения горя­чей воды в подводящих линиях u = 0,3 м/с, а температура воды t = 80°С. Как изменятся потери давления, если трубы соединить диффузо­ром с углом конусности a = 15° и шероховатостью K = 0,15 мм?

Ответ: D p» 38 Па; уменьшатся примерно в 2,5 раза.

Задача 2. В трубопроводе по перекачке воды для деления потока установлена приточная крестовина. Определить величину потери давления потока в прямом проходе и в боковых ответвлениях относи­тельно сборного рукава крестовины, если известно: угол боковых ответвлений d = 90°; d _б1 = d _б2 = d _б = 10 см; d _с = d _п = 15 см, М _с = 100 т/ч, М _б/ М _с = 0,35, температура воды t = 20°С.

Ответ: D p _с.б» 2 кПа; D p _с.п» – 0,18 кПа

Задача 3. Для повышения избыточного давления на трубопроводе диаметром d = 0,1 м установлена дроссельная шайба (диафрагма) d ₀ = 0,05 м. Определить величину потери давления в шайбе, если скорость воздуха в трубопроводе составляет u = 20 м/с, а температура t = 20^оС.

Ответ: D p» 7,2 кПа

Дата добавления: 2015-10-29