Гидравлический удар в трубах

При неустановившемся движении жидкости в трубах изменение во время скорости течения приводит к колебаниям давления, которое называется гидравлическим ударом. Теория этого явления разработана Н. Е. Жуковским. Простейшим случаем гидравлического удара являет­ся прямой удар, наблюдаемый при мгновенном перекрытии трубы.

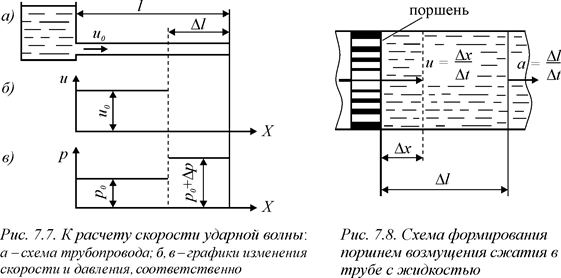
Рассмотрим трубопровод длиной l и сечением S, по которому со скоростью u _о течет жидкость, находящаяся под давлением p _o (рис. 7.7 а). При резком (мгновенном) закрытии задвижки ближайшие в ней частицы останавливаются. Их кинетическая энергия переходит в работу сжатия жидкости и деформации стенок трубы. Граница раздела сжатого остановившегося объема жидкости – ударная волна – распространяется навстречу втекающей невозмущенной жидкости.

Пусть за время ∆ t ударная волна проходит путь ∆ l. Скорость и дав­ление по длине трубы в момент времени, отделенный интервалом ∆ t от момента закрытия задвижки, представлены графически на рис. 7.7 б, в. Из рисунка ясно, что ударная волна является поверхностью разрыва для скорости и давления в трубе.

Определим величину ударного давления ∆ p, т. е. превышение давле­ния в сжатом объеме над невозмущенным давлением p _о. Для этого при­меним к объему остановленной жидкости S ∆ l теорему об изменении импульса:

D(mu)/D t = f. (7.22)

Вследствие малой сжимаемости капельных жидкостей и большой жесткости стенок трубы можно считать, что масса жидкости за время ∆ t внутри остановившегося объема не изменялась; она равна m = r S ∆ l. Изменение скорости составляет ∆ u ═ u _о − 0 = u _о. Сила f, вызванная из­менением импульса, есть разность давлений на торцевых поверхностях выбранного объема:

f = (p_o + ∆p) S – p_o S = ∆p S.

Подставляя эти величины в уравнение (7.22), имеем

r u _о∆ l /D t = ∆p. (7.23)

Учитывая, что ∆ l /D t = c есть скорость распространения ударной волны, получаем формулу Жуковского:

∆ p = ρ u _о c. (7.24)

Отметим, что величина ударного давления при прямом ударе не зависит от длины трубы l.

В тоже время скорость c зависит от упругих свойств жидкости и трубопровода.

В трубе с абсолютно жесткими стенками скорость ударной волны равна скорости распространения упругих колебаний (звука). Выведем ее величину.

Представим себе, что в жидкость, заполняющую трубу (рис. 7.8) и имеющую модуль объемной упругости E, вносится возмущение сжатия за счет движения поршня. Пусть за время ∆ t после начала движения поршень проходит путь ∆ x. За то же время волна сжатия, которая отделяет невозмущенную, покоящуюся жидкость от начавшей двига­ться со скоростью поршня, проходит расстояние ∆ l. Мы предполагаем, что возмущение слабое, т. е. ∆ x << ∆ l.

Сила, с которой поршень сжимает возмущенный объем, пропорцио­нальна его относительному сжатию

f = E S ∆ x /∆ l. (7.25)

С другой стороны, эту силу можно определить по изменению импу­льса в объеме S ∆l, применяя уравнение (7.22). Поскольку возмущение слабое, плотность можно считать неизменной и m = ρ S ∆l.

Изменение скорости:

.

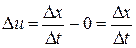Следовательно,

,

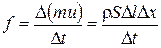что совместно с (7.25) дает

.

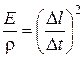Но ∆ l /D t есть скорость распространения волны возмущения в непо­движной жидкости a. Следовательно,

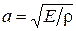. (7.26)

Исключим из уравнения (7.26) модуль объемной упругости жидкости E. По закону Гука, изменение объема V = S ∆l связано с изменением давления ∆ p соотношением:

,

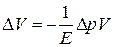или

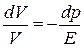. (7.27)

Поскольку масса жидкости внутри возмущенного объема не меняется при прохождении волны сжатия (уменьшение объема компенсируется увеличением плотности), очевидно, что ρ V = const. Логарифмируя и дифференцируя это равенство, получаем:

.

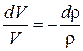Сравнивая с выражением, полученным ранее из закона Гука (7.27), имеем:

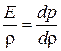. (7.28)

С учетом (7.28), формула (7.26) для скорости звука примет вид:

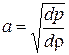. (7.29)

Как видим, скорость звука зависит от отношения возмущений дав­ления и плотности. Она определяется физическими свойствами жидкости [формула (7.26)]. Для воды, например, скорость звука равна примерно 1420 м/с, для нефти – около 1200 м/с.

В случае трубы с деформируемыми стенками скорость ударной волны несколько меньше скорости звука. Она определяется формулой

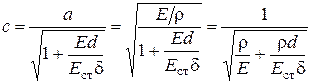, (7.30)

где E _ст – модуль объемной упругости (модуль Юнга) для материала стенки трубы, d – диаметр, d – толщина стенки.

Дата добавления: 2015-10-29