Гидравлический расчет трубопроводов

Различают простые трубопроводы, не имеющие боковых ответвлений, и сложные - с ответвлениями.

Короткими называют трубопроводы, в которых местные потери напора превышают 10% от потерь напора по длине. В противном случае трубопроводы считаются длинными. При их расчете местными потерями напора пренебрегают, а полную потерю напора получают завышением потерь по длине на 5-10%.

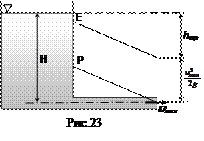При истечении жидкости по простому короткому трубопроводу в атмосферу (рис.23) уравнение Бернулли, записанное для свободной поверхности в баке и для выходного сечения с некоторыми допущениями, принимает вид

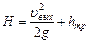(3.9)

Из этого следует, что при истечении в атмосферу действующий напор Н равен сумме удельной кинетической энергии u ²/2 g жидкости на выходе из трубопровода и полных потерь напора h_тр, то есть тратится на разгон жидкости до скорости u и преодоление гидравлических сопротивлений. Суммарная потеря напора h_т выражается по формулам (3.1), (3.2), (3.7), а в скоростном напоре на выходе из трубы учитывается формула средней скорости . После подстановок в уравнение (3.9) получим основную расчетную формулу

(3.10)

где 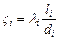- коэффициент гидравлического сопротивления на i -м участке трубопровода;

x_j – коэффициент местного сопротивления на j -м узле.

Следует заметить, что при истечении под уровень (рис.24), когда скоростью жидкости на выходе (во втором баке) можно пренебречь (u»0) и скоростной напор не учитывается, разность уровней в резервуарах целиком расходуется (тратится) только на преодоление гидравлических сопротивлений (D z = h_тр).

Расчет трубопроводов по уравнению (3.10) сводится к трем типовым задачам по определению:

1) напора Н; 2) расхода Q; 3) диаметра трубы d.

Задача первого типа решается прямым вычислением после определения числа Рейнольдса Re и коэффициентов l и x. Для определения числа Re требуется знать скорость течения, которая задается или вычисляется. По значению числа Рейнольдса определяется режим течения и область сопротивления, в зависимости от которых выбирается та или иная формула для расчета коэффициента гидравлического трения l. Далее рассчитываются потери напора и, в зависимости от типа истечения (под уровень или в атмосферу), определяется напор H.

Задача второго типа решается методом последовательных приближений или графоаналитически путем построения графика H = H (Q), так как l и x могут зависеть от числа Рейнольдса Re и, следовательно, от расхода Q.

Задача третьего типа решается методом подбора или графоаналитически путем построения кривой d = d (H).

3.4. Контрольные задания по разделу "Расчет трубопроводов"

Задача 1.

Два резервуара соединены простым трубопроводом диаметром d и длиной L (рис.25) По нему происходит истечение под уровень с расходом Q. Требуется найти разность уровней воды в резервуарах.

Местными сопротивлениями пренебречь. Кинематический коэффициент вязкости n принять равным 1.006×10^-6 м²/с

Исходные данные приведены в таблице 5.

Таблица 5.

№ варианта	Длина L, м	Диаметр d, мм	Расход Q, л/с
			1,1
			2,4
			3,5
			1,6
			1,2
			2,4
			1,0
			3,0
			2,5
			8,1

Задача 2.

По простому трубопроводу переменного диаметра происходитистечение в атмосферу (рис.26). Длина и диаметр первой и второй труб равны, соответственно l ₁, d ₁ и l ₂, d ₂.Трубопровод присоединен к резервуару под прямым углом. На одном из участков имеется задвижка. Учесть открытие задвижки, которое равно a, по данным приложения (П.2) Эквивалентная шероховатость D на обоих участках одинакова и равна 0,5 мм.

Кинематический коэффициент вязкости n принять равным 1.006×10^-6 м²/с.

Требуется:

1) найти напор H, необходимый для пропуска заданного расхода Q;

2) построить в масштабе пьезометрическую и напорную линии.

Исходные данные приведены в таблице 6.

Таблица 6.

№ вар	d1, мм	l1, м	d2, мм	l2, м	a, мм	Q, л/с
						8,5
						7,8
						18,3
						9,3
						19,3
						5,3
						6,3
						21,0
						5,2

Рекомендуемая литература

1. Штеренлихт Д.В. Гидравлика. Учебник для вузов. – 3-е изд., перераб. и доп. – М.: КолосС, 2005. – 656 с.

2. Лапшев Н.Н. Гидравлика. Учебник для вузов. – М.: Академия, 2007. – 268 с.

3. Ухин Б.В. Гидравлика. Учебное пособие для вузов. – М.: ИД «Форум»: Инфра-М, 2009. – 464 с.

4. Земцов В.М. Гидравлика. Учебное пособие для вузов. – М.: Изд-во Ассоциации строительных вузов, 2007. – 350 с.

5. Кудинов В.А., Карташов Э.М. Гидравлика. Учебное пособие для вузов. – 2-е изд., перераб. и доп. – М.: Высшая школа, 2007. – 198 с.

6. Чугаев Р.Р. Гидравлика: Учебник для вузов. - 4-е изд., перераб. и доп. – Л.: Энергоиздат, 1982. – 672 с.

7. Киселев П.Г. Гидравлика: Учебник для вузов – М.: Энергия. 1980.

8. Альтшуль А.Д. Примеры расчетов по гидравлике. – М.: Стройиздат, 1977.

9. Рабинович Е.З. Гидравлика. Учебник для вузов. – М.: Недра, 1980. – 278 с.

ПРИЛОЖЕНИЯ

Таблица П.1

Часто встречающиеся значения коэффициентов местного сопротивления

Наименование местного сопротивления	xj
Вход в трубу при нескругленных кромках	0.50
Вход в трубу со скругленными кромками	~0.20
Резкое расширение трубы (D 2 > D 1)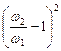
Резкое сужение трубы (D 2 < D 1)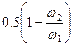
Переходный расширяющийся конус (при D 2»2 D 1)	~5.0
Переходный сужающийся конус (при D 2»0.5 D 1)	~0.20
Резкий поворот трубы на 90°	~1.20
Плавный поворот трубы на 90° (при D /2 R 0=0.2 - 0.6)	~0.15
Задвижка при полном открытии	0.15

Таблица П.2

Значения x _з для простой задвижки, перекрывающей круглоцилиндрическую трубу

a / D		0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9
x з	-	35.0	10.0	4.6	2.06	0.98	0.44	0.17	0.06

Дата добавления: 2015-10-29