Сила давления жидкости на плоские поверхности

Так как давление в жидкости изменяется с глубиной по закону 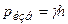, то на некоторой плоской погруженной поверхности будет распределено в общем случае неравномерно. Тем не менее, действие неравномерно распределенного гидростатического давления на может быть представлено суммарной силой давления F. Она равна произведению давления р_с (абсолютного или избыточного) в центре тяжести смоченной поверхности на площадь S этой поверхности

, (1.4)

где h_С - глубина погружения центра тяжести, м.

Например, сила давления жидкости на плоскую стенку АВ шириной b, перпендикулярную плоскости чертежа и наклоненную к горизонту под углом a (рис.3) будет равна

сила абсолютного гидростатического давления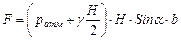

сила избыточного гидростатического давления .

где - заглубление центра тяжести С стенки АВ.

Если с другой стороны стенки также есть слой жидкости, то вычисляется сила давления жидкости со стороны этого слоя, а результирующая сила давления определится разностью сил от первого и второго слоев (рис.5,б)

Вектор силы F направлен перпендикулярно плоской поверхности. Точка D, через которую проходит вектор силы F, называется центром давления. Давление в соответствии с уравнением (1.1) возрастает с глубиной, поэтому центр давления D смещен в сторону наибольших давлений, то есть в общем случае находится ниже центра тяжести С (рис.4). Координата z_d центра давления для стенки любой формы определяется по формуле

(1.5)

где z_C - координата центра тяжести смоченной поверхности стенки;

I_C - момент инерции площади смоченной поверхности стенки относительно горизонтальной оси, перпендикулярной плоскости рисунка и проходящей через центр тяжести С, м⁴.

Для прямоугольной стенки, верхняя кромка которой совпадает со свободной поверхностью, I_C = bz ³/12, S=bz, z_C = z /2. Поэтому из формулы (1.5) получаем z_D =2/3 z, то есть центр давления D находится от свободной поверхности на расстоянии 2/3 z в плоскости стенки или на расстоянии 2/3 Н по вертикали.

Давление на прямоугольную стенку удобно определять графически с помощью эпюры давления, - фигуры, которая характеризует распределение избыточного давления на плоской поверхности. На рис.5,а эпюра давления, действующего на вертикальную плоскую стенку ОВ (щит гидротехнического затвора, стенку канала или гидравлического лотка и т.п.) представлена треугольником АОВ. Она показывает, что избыточное давление жидкости на стенку распределяется по гидростатическому закону p = gh, изменяя значения от 0 до gH. На рис.5,б сила давления представляется разностью эпюр давления жидкости с двух сторон стенки. Эпюра суммарной силы давления F изображается в данном случае трапецией NMOB. Площадь эпюры численно равна силе давления, которая действует на единицу ширины стенки. Общий вектор силы давления F направлен перпендикулярно стенке и проходит через центр тяжести эпюры.

Дата добавления: 2015-10-29