Истечение жидкости и газа через отверстия и насадки

Истечение (выход) жидкостей (газов) из аппаратов и резервуаров происходит через отверстия или насадки (штуцеры), расположенные в днищах или боковых стенка. При этом необходимо знать расход жидкости (газа) в единицу времени при непрерывном истечении из отверстия. Данная задача, как показано ниже, решается с помощью уравнения Бернулли.

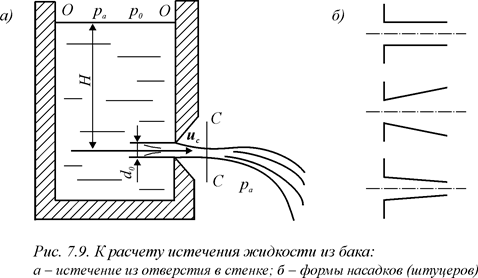
Истечение жидкости через отверстия и насадки. Рассмотрим истечение жидкости из бака через небольшое отверстие с острыми кромками (рис. 7.9 а).

Опыт показывает, что струя имеет меньший диаметр, чем отверс­тие. Это сжатие струи происходит главным образом вследствие дейст­вия центробежных сил на частицы, движущиеся из бака к отверстию по криволинейным траекториям. На расстоянии от выходной кромки порядка d ₀/2 (d_o – диаметр отверстия) сжатие струйки можно считать неизменным. Отношение площадей сжатого сечения струи S _c и отверстия S называют коэффициентом сжатия струи:

e = S _c / S. (7.41)

Определим скорость струи в сжатом сечении С – С. Для этого при­меним к струйке, начинающейся от поверхности жидкости в баке (сечения О – О), уравнение Бернулли

.

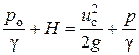Мы пренебрегли скоростным напором u ₀²/(2 g) ввиду малой скорости падения уровня в баке в сравнении со скоростью истечения; жидкость считаем идеальной.

Если p = p _o, то u _c²/(2 g) = H, откуда скорость струи определяется формулой Торичелли:

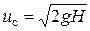. (7.42)

Как видим, скорость истечения идеальной жидкости равна скорости свободного падения тела в пустоте с высоты H.

Если давление над поверхностью в баке и в пространстве, в которое вытекает струя, неодинаково, то из уравнения следует:

,

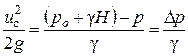откуда

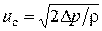, (7.43)

где Δ p – разность давлений на уровне оси отверстия.

Для реальной жидкости из-за вязкого трения скорость струи оказы­вается несколько меньше теоретической. Влияние трения учитывают введением в формулу (7.42) (для формулы (7.43) дальнейшие измене­ния аналогичны) коэффициента скорости истечения φ < 1, так что

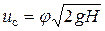, (7.42а)

По опытным данным, при истечении воды и воздуха φ ≈ 0,97–0,98, т.е. вязкое трение снижает скорость истечения на 2–3% [1].

Тогда, действительный объемный расход жидкости при истечении из отверстия, с учетом формулы (7.41) выразится так:

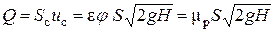. (7.44)

Величина m_р = e φ, называемая коэффициентом расхода, зависит от формы отверстия, отношения площадей S _c / S и числа Re и определяется опытным путем; для круглых отверстий в среднем m_р = 0,62 [12].

Коэффициент расхода m_р значительно возрастает при истечении жидкости через насадок (штуцер), представляющий собой короткую трубку, приставленную к отверстию (рис. 7.9 б), длина которой в 3,5–4 раза больше диаметра отверстия. Струя при выходе из отверстия в насадок сжимается, но приказанной его длине успевает расширяться и вытекает полным сечением. Однако и в данном случае m_р < 1 вследст­вие потери напора при входе в насадок и последующем расширении струи. Например, при истечении воды для цилиндрического насадка m_р = 0,82; для расширяющегося конического m_р = 0,45; для сходящегося конического (с углом при вершине» 13°) m_р = 0,963 [4].

При малых перепадах давления Δ p (порядка нескольких процентов от исходного давления p _o) формулы для расчета скорости истечения несжимаемой жидкости применимы и для газов. В этом случае не учет сжимаемости газов не приводит к существенным ошибкам. При значительных перепадах давления скорость истечения газа определяют по формулам газодинамики, которые рассмотрены далее.

Истечение сжимаемого газа. При истечении газа (пара, воздуха) в окружающую среду под высоким давлением резко изменяется его объем. Поэтому необходимо учитывать сжимаемость газа.

Исследуем адиабатическое истечение идеального газа из резервуара (пренебрегая потерями в насадке), где он находился под давлением р_о, в среду с давлением р.

Применяя к сечениям струйки газа в резервуаре, где скорость близка к нулю, и в сжатом сечении уравнение энергии в форме (4.12), имеет вид:

,

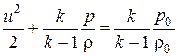откуда

.

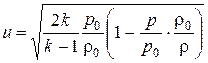Выражая r₀/r через p / p ₀ с помощью уравнения адиабаты (4.3) и используя уравнение состояния (4.2), получим формулу Сен-Венана и Венцеля для скорости адиабатного истечения газа:

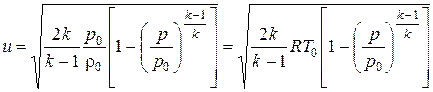. (7.45)

С уменьшением p / p ₀ скорость истечения u возрастает до тех пор, пока не достигнет критического значения. Критической называется скорость течения, равная местной скорости звука. Величину критиче­ской скорости легко определить из уравнения энергии в форме (4.12в) или (4.12г), если принять u = a = a _кр:

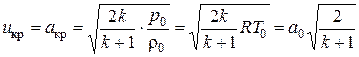, (7.46)

при это критическое отношение давлений равно:

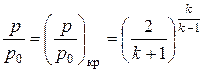. (7.46а)

В частности, для воздуха, при температуру 15°C, a _кр = 0,91 a ₀ = 310 м/с. При дальнейшем уменьшении внешнего давления p скорость истечения остается неизменной и равной α _кр .

Массовый расход M газа при истечении из отверстия с учетом по­терь в насадке (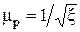 [12]) для случая, когда p / p ₀ ³ (p / p ₀)_кр , равен:

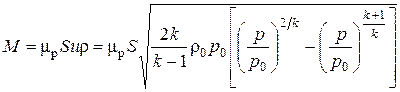. (7.47)

При p / p ₀ < (p / p ₀)_кр выражение для M имеет вид

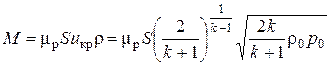. (7.47а)

Массовый расход в этом случае от внешнего давления p не зависит, а определяется давлением p ₀ в резервуаре, возрастая с его увеличением.

Дата добавления: 2015-10-29