Формулировка задачи

Суть математической формулировки задач линейного программирования сводится к определению экстремума линейной функции конечного числа неотрицательных аргументов, связанных между собой системой линейных ограничений, а именно функции следующего вида:

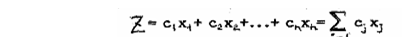
Содержательная формулировка транспортной задачи выглядит следующим образом:

Пусть в пунктах А₁, А₂,..., А_m производится некоторый однородный продукт, причём, объём производства этого продукта в пункте A_i‚ составляет а_i единиц, i = 1,...,m.

Произведённый в пунктах производства продукт требуется доставить в пункты потребления В₁, В₂,..., В_n, причём объём потребления в пункте В_j составляет b_j единиц продукта.

Предполагается, что транспортировка готовой продукции возможна из любого пункта производства в любой пункт потребления и транспортные издержки, приходящиеся на перевозку единицы продукта из пункта А_i в пункт В_j, составляют a_i денежных единиц, i =1,...,m.

Задача состоит в организации такого плана перевозок, при котором суммарные транспортные издержки были бы минимальными.

Формальная постановка «транспортной задачи».

Пусть x_ij - количество продукта, перевозимого из пункта А_i в пункт В_j. Требуется определить совокупность из mn величин х_ij, удовлетворяющих условиям:

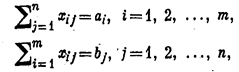
и обращающих в минимум линейную форму:

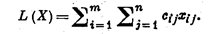
Для решения «транспортной задачи» воспользуемся симплекс–методом, («симплекс» - в переводе означает «простой», то есть несложный).

Суть метода состоит в приведении задачи к так называемому стандартному виду, при котором обеспечивается равенство ресурсов и потребностей. При этом используется табличная матрица, следующего вида:

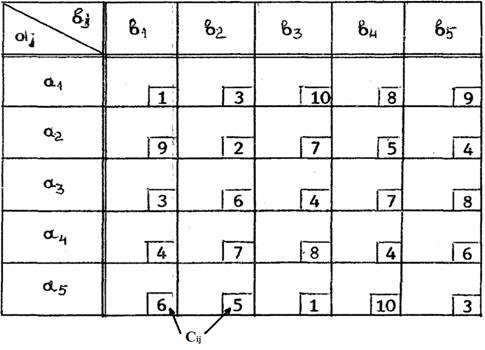
Рис. 3.1. Общий вид распределительной матрицы

На рис 3.1. с_ij - это единичная стоимость, т.е. стоимость перевозки единицы груза от i -го поставщика j -му потребителю.

Все преобразования симплекс-метода мы также будем проводить непосредственно в табличной матрице. Каждое очередное преобразование (итерация, что в переводе означает «шаг») будет продуцировать новый план перевозок, с уменьшенным значением целевой функции. Преобразования-итерации заканчиваются достижением оптимума. Для этого используются два метода: распределительный метод и метод потенциалов.

Каждый из названных методов приводит к оптимальному решению.

Каждый из алгоритмов по названным двум методам начинается с построения опорного решения, оно является исходным, с которого начинаем реализацию алгоритма. Нахождение опорного решение строится образом, что в нём число заполненных клеток должно равняться рангу системы r:

r = p+ q – 1 (3.4)

Для нахождения опорного решения имеются два метода: метод северо-западного угла и метод минимального элемента.

При этом формулируются и следующие ограничения:

- значения переменных х _ij должны быть больше или равны нулю, поскольку отрицательными объёмы перевозок быть не могут;

- остаётся в силе приведенное определение ранга системы.

Заметим, что общее число базисных решений, которые могут удовлетворять записанным уравнениям составляет N_б:

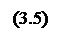
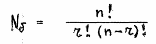
где: n - общее число переменных x;

r – ранг системы.

Если мы найдём все базисные решения данной системы, то среди них окажутся и такие, в которых базисные переменные будут положительными. Такие решения называют опорными решениями. При проведении итераций в распределительной таблице следует помнить, что нули базисных переменных обязательно записываются в свободные клетки, в отличие от нулей свободных переменных, которые имитируются пустыми клетками.

Обычно такие базисные нули фигурируют в угловых клетках цикла, и без их использования невозможно организовать целенаправленного циклического преобразования.

В целом методика решения данной задачи осуществляется в следующей последовательности:

1. Находим одним из двух методов исходное опорное решение системы,

2. Осуществляем цепочку последовательных циклических преобразований опорного решения симплекс-методом, достигая уменьшения целевой функции.

3. Останавливаем процесс при достижении Z_min.

3.2.Нахождение опорного решения методом «северо-западного угла»

Реализацию метода целесообразно пояснить на примере (рис 3.2).

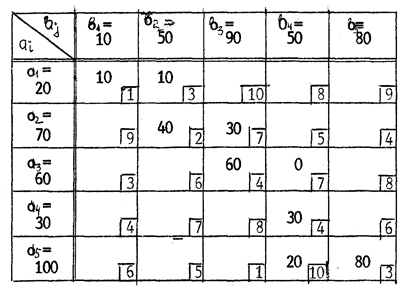
Рис. 3.2. Опорное решение, полученное по методу «северо-западного угла»

Сущность метода «северо-западного угла» заключается в том, что на каждом очередном этапе или максимально исчерпываются ресурсы отправителей, или максимально удовлетворяются потребности потребителей.

Целевая функция для матрицы (рис. 3.2) составляет Z₁ = 1130.

Последовательность действий при заполнении представленной выше матрицы следующая:

· распределение ресурсов начинается с клетки, расположенной на «северо-западе», то есть в левом верхнем углу. Ей соответствует ресурс а₁ = 20 и потребность b₁ = 10. Удовлетворяем потребность полностью, остаётся ресурс, равный 10;

· затем, по правилу, «дораспределяется» остаток ресурса, передав его следующей потребности b₂ которая его забирает, но с нехваткой относительно её потребности;

· нехватка ресурса для потребности b₂ восполняется уже за счёт ресурса a₂, расположенного уже во второй строчке таблицы;

· действия повторяются таким же образом и далее, с образованием ряда ступенек, ведущих в правый нижний угол, где и заканчивается процесс начального распределения.

При нахождении опорного решения данным образом следует иметь в виду, что иногда на некоторой клетке таблицы одновременно заканчиваются и ресурсы, и потребности. Тогда для дальнейшего продвижения (по правилам расчёта) записывается базисный ноль - либо в последующей клетке той же строчки, либо в последующей клеточке того же столбца.

В законченном расчёте любого опорного решения количество заполненных клеток должно быть равно рангу системы (r). В противном случае, реализация алгоритма нахождения опорного решения становится невозможной.

Как первое, так и все последующие решения являются возможными для практического осуществления, а эффективность каждого оценивается значением целевой функции. Целевая функция практически служит критерием эффективности того или иного плана, записанного в виде корреспонденций груза в каждой клеточке распределительной таблицы.

3.3. Нахождение опорного решения методом «минимального элемента»

Метод «минимального элемента» строится на том же принципе исчерпания ресурсов для обеспечения потребностей, но есть одна разница.

Сущность метода предлагаемого метода сводится к тому, что, в отличие от метода северо-западного угла, последовательное исчерпание ресурсов за счёт потребностей проводится, через клетки, в уголках которых находятся (по возможности) наименьшие значения единичной стоимости.

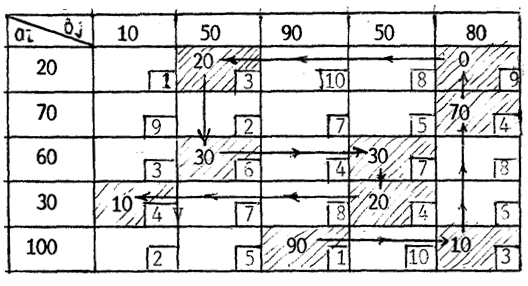Рис. 3.3. Опорное решение, полученное по методу «минимального элемента»

Целевая функция для матрицы (рис. 3.3) составляет Z₂ = 970.

Стрелками показан маршрут прохождения клеток с минимальными элементами, начиная с самой выгодной минимальной клетки. Метод минимального элемента, в данной задаче, обеспечил меньшее значение целевой функции, чем метод «северо-западного угла». Таким образом, была сокращена трудоёмкость расчётов.

Контрольные вопросы

1. В чем состоит сущность транспортной задачи линейного программирования?

2. Какой показатель эффективности используется в транспортной задаче?

3. Что такое «ранг системы»?

4. Какие ограничения устанавливаются при решении транспортной задачи?

5. Опишите общую методику решения транспортной задачи

6. Охарактеризуйте особенности метода «северо-западного угла»

7. Охарактеризуйте особенности метода «минимального элемента»

Лекция 4

Дата добавления: 2015-10-29