Непрерывная случайная величина

Непрерывная случайная величина характеризуется тем, что её реализации в виде численных значений могут находиться в любой точке интервала: от минимальной до максимальной границы его значений.

Более строгое определение непрерывной случайной величины следующее: Случайную величину Х называют непрерывной (непрерывно распределенной) величиной, если существует такая неотрицательная функция p (t), определенная на всей числовой оси, что для всех х функция распределения случайной величины F (x) равна:

При этом функция p (t) называется плотностью распределения вероятностей непрерывной случайной величины.

Если такой функции p (t) не существует, то Х не является непрерывно распределенной случайной величиной.

Непрерывная случайная величина характеризуется дифференциальной и интегральной функциями распределения вероятностей.

Наиболее широко в практике исследований для обобщения случайных процессов применяется «нормальное распределение плотностей вероятностей». Нормальное распределение (распределение Гаусса).

Дифференциальная функция распределения плотности вероятностей (для Нормального распределения) выражается формулой:

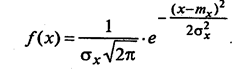
Интегральная функция распределения плотности распределения вероятностей выражается формулой:

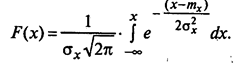
Контрольные вопросы

1. Какие модели относятся к вероятностным?

2. Что такое «случайная величина»?

3. Чем характеризуются массовые процессы?

4. Какие выделяют виды случайных процессов?

5. Дайте определение понятию «вероятность»

6. Что такое «процесс»?

7. Какие свойства систем наиболее важны при их исследовании?

8. Какова последовательность исследования системы практикуется в ИСО?

9. Задачами какого масштаба оперирует ИСО в процессе исследования систем?

10. Охарактеризуйте понятие «дискретная случайная величина».

11. Охарактеризуйте понятие «непрерывная случайная величина».

Лекция 8

Дата добавления: 2015-10-29