Методика оптимизации сетевых моделей

Поэтому на основе анализа первого варианта сетевого были разработаны предложения по дополнительному вводу двух устройств налива (загрузки) и одного устройства для разогрева продукта (рис.6.7). (позиции нововведений на новом графике обозначены подчёркиванием).

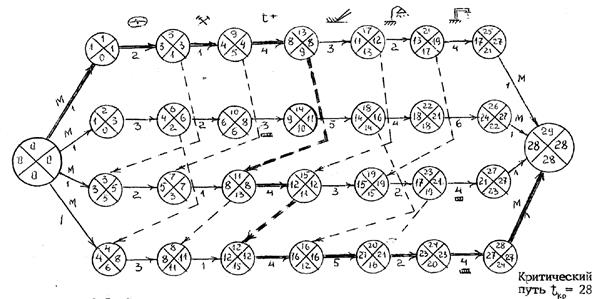
Рис. 6.7. Законченный вид сетевого графика (вариант № 2)

На основе приведенного примера можно судить о достоинствах сетевой модели сетевого планирования и управления.

Использование информационных технологий открывает перспективы быстрого просчёта вариантов и наглядного представления всех процессов.

Отметим также, что сетевой график представляет собой систему, которая поддаётся декомпозиции на отдельные модули.

Учитывая такие возможности, можно разрабатывать номенклатуру сетевых моделей для крупных задач различного назначения.

Номенклатура модулей может быть разработана на тех же принципах, что и номенклатура географических карт.

Известны также опыты разработки сетевых моделей, в которых разработаны алгоритмы расчёта сетевых моделей с вероятностными оценками продолжительности отдельных работ сетевого графика и сетевой модели в целом.

Поскольку сетевые модели широко применяются в США и других странах для выполнения самых сложных и ответственных проектов, то сомнений в перспективности этого направления не возникает.

Контрольные вопросы

1. Какой наиболее распространенный метод, применяемый для построения сетевых моделей?

2. Охарактеризуйте каждый из секторов «события» в графоаналитической сетевой модели.

3. Каков порядок заполнения секторов в вершинах сетевого графика в графоаналитической модели?

4. Раскройте сущность понятия «критический путь».

5. Что показывает «резерв времени»?

6. Какие правила необходимо знать при построении сетевой модели?

7. Каким образом проводится оптимизация сетевой модели?

8. Что является показателем эффективности оптимизации сетевой модели?

Лекция 7

Вероятностные модели исследования операций. дискретная случайная величина. непрерывная случайная величина

План

7.1. Терминология

7.2. Принципы исследования систем

7.3. Дискретная случайная величина

7.4. Непрерывная случайная величина

Терминология

Для математических формализаций множества транспортных процессов используются «случайные величины».

Случайная величина - одно из основных понятий теории вероятностей. В самом общем смысле – это некоторая переменная величина, принимающая, в зависимости от случая, те или иные значения с определёнными вероятностями.

Использование случайной величины, как понятия, тесно связано с практикой обобщения закономерностей тех массовых процессов, проявления которых характеризуются устойчивостью. Массовый процесс характерен тем, что он имеет достаточно большое количество реализаций, каждая из которых может быть измерена и зарегистрирована. Совокупность таких данных называется статистической выборкой. Статистическая выборка представляет собой массив данных, которые характеризуют процесс.

Здесь необходимо сказать о том, что различают два вида случайных процессов, а именно:

1) случайный процесс, реализации которого представляют собой последовательность измеренных значений какого либо параметра процесса, актуального для решения практических задач;

2) случайный процесс, реализации которого представляют собой актуальные для аналитика события, которые в очередном наблюдении, могут: либо быть отмечены, либо отсутствовать.

Для получения данных используется статистический эксперимент, то есть специально организованная система измерений и наблюдений реализаций процесса.

Случайная величина характеризуется всеми своими реализациями, если рассуждать теоретически, но практически используется только их часть.

Но таких измерений необходимо провести достаточно много, чтобы проверить близость значений параметров случайной величины и убедиться в устойчивости наблюдаемого процесса.

Элементарные понятия о случайных событиях, величинах и функциях в математике сводятся к следующим определениям:

Под событием понимается всякий факт, который может произойти или не произойти в очередном наблюдении (испытании).

Теория вероятностей рассматривает события в тесной связи с теми условиями, в которых они наступают.

Совокупность условий, которые определяют закономерности проявлений вероятностного (случайного) процесса называется комплексом основных условий.

Системно организованное наблюдение реального вероятностного процесса называется статистическим экспериментом.

При этом подразумевают, что число зарегистрированных реализаций случайного процесса должно быть достаточным, чтобы охарактеризовать закономерности процесса. То есть статистическая выборка должна быть достаточно представительна.

Формально различают события достоверные и события невозможные.

Достоверным называется такое событие, которое наступает при каждом испытании.

К вероятностным процессам относятся только устойчивые массовые процессы. И только к таким процессам можно применять все математические методы исследования, разработанные в теории вероятностей.

Устойчивая частость - называется вероятностью.

Вероятность — степень (относительная мера, количественная оценка) возможности наступления некоторого события при определенных условиях

Вопрос устойчивости частостей является очень важным для анализа реальных процессов. Это касается как оценок вероятностных процессов, оцениваемых посредством непрерывной случайной величины, так и процессов, которые оцениваются посредством дискретной случайной величины.

В исследовании процессов, которые обобщаются непрерывной случайной величиной, устойчивость выражается в устойчивости параметров гистограмм, то есть графиков частостей. Последние в практике использования результатов обычно заменяются близкими по содержанию теоретическими графиками плотности распределения вероятностей.

Принципы анализа реальных процессов на основе теории вероятности сильно отличаются от использования других привычных математических моделей.

Если мы пользуемся, например, моделями линейного программирования или математическими алгоритмами линейной алгебры, то получаем численные результаты, в истинности которых не приходится сомневаться.

При использовании моделей теории вероятностей, в абсолютном большинстве случаев, мы имеем приблизительное сходство математических зависимостей с реальными закономерностями процессов, которые ими обобщаются.

В использовании математического аппарата теории вероятности используется принцип практической применимости математических моделей, дополненных специальными оценками, которые служат для оценки погрешности теоретических обобщений по отношению к реальным процессам.

Дата добавления: 2015-10-29