Описание алгоритма однократного замещения

Распределительная таблица фактически является матрицей, с которой можно проводить преобразования и получать новые опорные решения используя метод однократного замещения Жордана-Гаусса, сущность которого сводится к назначению другой базисной переменной, вместо одной из свободных.

При таком замещении свободная переменная объявляется базисной и подлежит определению, а некоторая базисная (безразлично какая) становится свободной. В математике доказано, что в каждом опорном решении задачи линейного программирования, размещённом в распределительной таблице, можно построить цикл, (и притом только один), однократного замещения одной свободной переменной на одну базисную переменную. При этом продуцируется новый опорный план с новым значением целевой функции. Матрица «единичных стоимостей», обеспечивает общий расчёт затрат по любому полученному решению. То есть она обеспечивает оценку решения записанного в таблице.

При целенаправленном преобразовании начальной таблицы-матрицы можно достигать как минимизации затрат. Рассмотрим методику названного алгоритма.

Циклом называют набор клеток, в котором две и только две клетки расположены в одной строке или в одном столбце, причём, последняя клетка столбца образует первую клетку строки, и так далее, вплоть до замыкания цепочки в цикле (см. рис. 4.1).

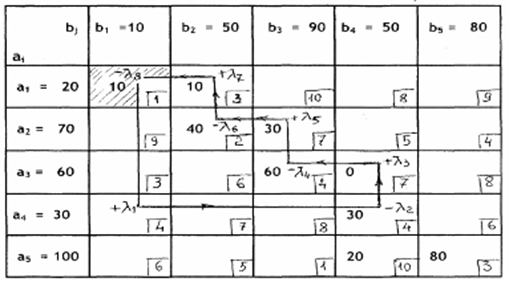
Рис. 4.1. Схема циклического преобразования

Целевая функция при этом равна Z₀= 1130

С каждым опорным решением можно провести циклическое преобразование, которое всегда начинается в одной из свободных клеток, затем проходит только через занятые клетки, и заканчивается на исходной клетке.

Число вариантов таких преобразований равно числу свободных клеток. Число занятых клеток всегда должно быть равно рангу системы.

Приводим пример проведения циклического преобразования со свободной клеткой 4-1 (координаты клеток определяются номерами индексов переменных). Построим «от неё» схему цикла однократного замещения, изобразив его в таблице найденного ранее исходного («нулевого») варианта опорного решения.

В свободной клетке (4-4) размещаем +λ₁ (первая нечётная порядковая клетка). Протягиваем далее от неё стрелку до занятой клетки (4-4), где будет размещаться - λ₂... далее поступаем аналогичным образом, чередуя положительные и отрицательные значения λ_m, размещённые в угловых клетках, согласно последовательности построения цикла. Заметим, что индексы фиксируют только порядковое расположение λ, и к его численному значению никакого отношения не имеет. Численное значение λ определяется после построения цикла. Правила построение циклов всегда обеспечивают равное количество отрицательных и положительных по знаку значений λ_m..

Для выполнения очередного циклического преобразования достаточно выбрать клетку, которая, в построенном начальном цикле, имеет наименьшее, (по абсолютной величине), значение переменной, и находится в углу цикла со знаком «минус». В нашем примере это клетка 1-1 (рис. 4.2.).

3начение величины λ определяем (см. рис 4.2) следующим образом:

1) выберем в углах цикла клетку, с наименьшим размером корреспонденции, это будет клетка (1-1) с корреспонденцией λ₁₁= 10;

2) выполним одно преобразование однократного замещения;

3) определим оценку клетки: О_4-1 = +4 -4 +7-4+7-2+3-1 = 21-11 = +10

4) далее, можно определить ΔZ₁ = λ · О₁ = (+10)· (+10) = 100.

5) делаем вывод, что выбранная клетка (4-1) не обеспечивает уменьшение целевой функции Z. (Z₁ >Z₀), и от преобразования с ней надо отказаться. Выбираем следующую клетку... и так далее, пока не найдём клетку с отрицательной оценкой.

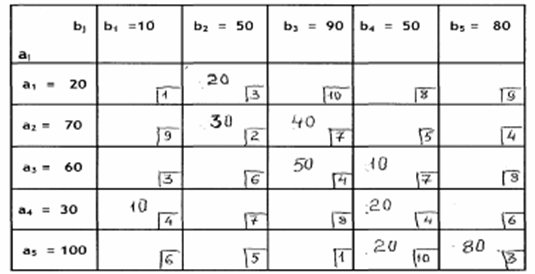
Z₁ = 1230; λ = + 10; О_4-1 = +10

Рис. 4.2. Табличная матрица после преобразования № 1

4.2. Метод «северо-западного угла»

Для того чтобы заранее определить, будет ли вести новое решение, к уменьшению значения целевой функции, мы прибегаем к расчёту оценки свободной клетки на предмет полезности её использования для получения нового опорного решения с уменьшенным численным значением целевой функции.

Только в случае, когда выбранная клетка имеет отрицательное значение, то есть со знаком минус, новое решение, полученное на основе проведения алгоритма однократного замещения с выбранной свободной (пустой) клеткой, приведёт к решению с уменьшенным значением целевой функции Z_n, (здесь индекс «n» – означает порядковый номер реализуемого алгоритма однократного замещения).

Дата добавления: 2015-10-29