Основы теории графов

Сетевое планирование и управление (СПУ), или, проще, «сетевые графики» получили широкое распространение в отечественной практике благодаря наглядности этого вида графических моделей.

Теоретической основой для такого представления задач послужила теория графов.

Граф (от греческого 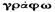- пишу) – это формализованное изображение, составленное из множества V вершин и набора E неупорядоченных и упорядоченных пар вершин. Обозначается граф через G(V, E). Неупорядоченная пара вершин связывается ребром, упорядоченная пара — связывается между собой дугой (дуга фигурирует вместе со стрелочкой, показывающей её направление). Граф, содержащий только рёбра, называют неориентированным, а содержащий только дуги, называют ориентированным. Пара вершин может соединяться двумя или более рёбрами (дугами одного направления), такие рёбра (дуги) называются кратными.

Дуга (или ребро) может начинаться и кончаться в одной и той же вершине, такая дуга (ребро) называется петлёй.

Вершины, соединённые ребром, или дугой, называют смежными.

Рёбра, имеющие общую вершину, также называют смежными, а любые из его двух вершин называются инцидентными.

Говорят, что ребро (u,v) соединяет вершины u и v, и говорят, что дуга (u,v) начинается в вершине «u» кончается в вершине «v».

Каждый граф можно представить в евклидовом пространстве множеством точек, соответствующих вершинам, которые соединены линиями, и эти вершины будут соответствовать ребрам.

Этот класс графов называется плоским, и именно он модифицирован для использования в расчётных моделях сетевого планирования и управления.

Отвлекаясь от содержательной стороны дела, можно рассматривать любой сетевой график как совокупность G некоторого количества точек X₁ Х₂,... и установленных между ними соответствий (связей).

То есть такой объект G называется графом, а точки Х₁, Х₂...— его вершинами, связи между ними - дугами. Граф G считается заданным, если заданы все его вершины и дуги

Рис. 5.1. Примеры графов

Ориентация дуг, т. е. указание «начала» и «конца» каждой из них, делает граф ориентированным (рис. 5.1. б). Любые две вершины называются смежными, если их соединяет дуга. Граф, в котором какие-то две вершины соединяются несколькими дугами, называется мультиграфом (рис. 5.1. в).

Особенности и постановка задач сетевого планирования

Рассматривать особенности построения сетевых моделей целесообразно на конкретном примере.

В качестве примера рассмотрим решение одной из проблем организации транспорта, а именно технологический график оборота специальных цистерн для перевозки затвердевающих грузов.

Рис. 5.2. Технологический процесс оборота вагонов-цистерн

Рассмотрим технологический процесс перевозки специальных грузов в железнодорожных вагонах-цистернах.

Перевозимый продукт представляет собой затвердевающую жидкость, которая загружается в расплавленном виде, а затем затвердевает. Загрузка идет под слой воды, который, затем, выполняет функции защитного компонента против самовозгорания.

Доставка таких грузов осуществляется партиями по 4 - 6 вагонов, в сопровождении проводников, по правилам, установленным для перевозок МПС.

Подвижной состав принадлежит заводу-изгоготовителю продукта, и он «оборачивается» по замкнутому кругу между изготовителем и получателем продукта.

Перед предприятием изготовителем продукта стоит задача сокращения времени оборота вагонов-цистерн, что обеспечивает повышение производительности перевозок и снижает затраты по подготовке к отправке подвижного состава.

Сетевая модель представляет собой последовательность операций (работ) в цикле оборота вагонов-цистерн.

Актуальной частью процесса является технология погрузки и выгрузки, а также обработки подвижного состава с выполнением сложных технологических операций.

Установлено, что в связи с ростом объёмов производства продукции необходимо соответствующим образом модернизировать систему обслуживания.

На основе обследования предприятия были получены сведения, которые характеризуют его техническое оснащение, производительность технологических устройств, систему организации обслуживания, историю развития и технического совершенствования системы. Сведения о структуре организации обслуживания сведены в табл. 12.2.1.

Таблица 5.1

Сведения о технологических постах обработки цистерн

продолжение таблицы 5.1

Установлено, что отправка продукции производится партиями по 4 вагона-цистерны, технологические имеют различную производительность, поступление в обработку подвижного состава не упорядочено.

Продолжительности обслуживания одинаковых по назначению постов различаются по времени (табл.5.1).

Для проведения анализа необходимо провести исследования реальной системы на основе использованием графоаналитической модели сетевого планирования и управления (СПУ).

Контрольные вопросы

1. Дайте определение понятию «граф»

2. В чем заключается основное различие между дугой и ребром графа?

3. Какие задачи транспорта целесообразно представлять в виде сетевых моделей?

4. Какие методы используют для исследования реальной системы на основе построения графа?

5. В чем заключаются особенности задач сетевого планирования?

Лекция 6

Дата добавления: 2015-10-29