Порядок проведения измерений и выполнения расчетов

Тарировка индукционного датчика

1. Подключить к лабораторному модулю соленоид.

2. Полностью ввести шток в соленоид.

3. Установить с помощью резистора с переменным сопротивлением максимально возможное значение тока соленоида и измерить значение ЭДС индукции.

4. Проделать 4 – 5 измерений ЭДС индукции, уменьшая каждый раз значение тока на 0,2 А. Результаты измерений занести в табл. 2.

Таблица 2.

I, A	, B	B, Tл	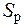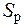, м^2	< >, м^2

5. Милливольтметр и миллиамперметр показывают действующие значения ЭДС и тока, которые в раз меньше амплитудных. Подставляя действующие значения токов в формулу (3), рассчитать соответствующие значения магнитной индукции, а затем значения 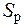для каждого значения тока, учитывая, что в соответствии с уравнением (7)

где – действующая ЭДС; В – значение магнитной индукции, рассчитанное по формуле (3), Тл

6. Вычислить среднеарифметическое значение площади измерительной рамки < 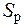>. Результат внести в табл. 2.

Определение магнитной индукции на оси соленоида

1. Установить значение тока соленоида, равное 1 А.

2. Полностью ввести шток в соленоид.

3. Перемещая шток на 1 деление (1 см), снять зависимость ЭДС от координаты. Результаты записать в табл. 3.

4. Рассчитать экспериментальные значения магнитной индукции по формуле

(8)

5. Рассчитать теоретическое значение магнитной индукции на оси соленоида по формуле (2) во всех точках, в которых производились измерения.

6. Построить графики = f (x) и = f (x) в одних координатных осях.

Таблица 3

х, см	, мВ	, Тл	, Тл
…

Определение магнитной индукции на оси короткой катушки

1. Установить значение тока катушки, равное 1 А

2. Установить шток в такое положение, чтобы вне соленоида находилось два деления штока. Перемещая шток вдоль соленоида, добиться максимального показания милливольтметра, присоединенного к рамке. В этом положении измерительная рамка на штоке оказывается в центре катушки (х = 0).

3. Перемещая шток каждый раз на 1 см, снять зависимость = f (x).

4. По формуле (8) рассчитать экспериментальное значение магнитной индукции на оси катушки для каждого значения координаты.

5. По формуле (6) рассчитать теоретическое значение магнитной индукции на оси катушки для каждого значения координаты.

6. Результаты измерений и расчетов записать в табл. 4.

7. Построить графики = f (x) и = f (x).

Таблица 4.

х, см	, мВ	, Тл	, Тл
-2 -1 …

ПРИЛОЖЕНИЕ

Выведем соотношение (2). Вычислим сначала индукцию магнитного поля на оси одного токонесущего кругового кольца, которую совместим с координатной осью х, поместив начало отсчета в плоскости кольца (рис.1п).

    х dB(x) от I dl θ r I dl   R 0    

Рис. 1п

Магнитное поле кругового тока обладает осевой симметрией. Это означает, в частности, что вектор В (х) в любой точке оси х «лежит» на этой оси, т.е. В (х) = { В_х (х); 0; 0}. Как видно из рис.1п, произвольный элемент I dl кругового тока дает в В_х (х) одинаковый вклад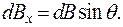

Поэтому интегрирование по всему кольцу в соответствии с формулой (1)

сводится к вычислению длины окружности радиуса R. Так что окончательная формула для одного витка принимает вид

(9)

где учтено очевидное равенство .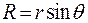

Переходя к катушке (см. левый из рис. 2п), допустимо предполагать, что электрический ток непрерывно распределен по цилиндрической поверхности и в элементарном поясе ширины dx равен где – погонное (приходящееся на единицу длины катушки) число витков намотки, а – ток одного витка. Произведение именуют числом ампервитков. Поле на оси катушки в точке M, создаваемоеэлементарным поясом, который виден из этой точки под углом , выражается формулой (9):

Интегрируя это выражение от до (см. правый из рис. 2п), получаем выражение магнитной индукции в точке М

.

Таким образом, подтверждено начало формулы (2). Геометрическую расшифровку косинусов, приводящую к последнему выражению в (2), легко получить с помощью правого верхнего рис. 2.

Контрольные вопросы

1. Чем создаются магнитные поля и на что они действуют?

2. Какой величиной характеризуется магнитное поле в точке пространства?

3. Что такое принцип суперпозиции полей?

4. Закон Био 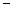Савара.

5. Способ измерения индукции магнитного поля, используемый в данной работе.

6. Принцип расчета поля, изложенный в приложении.

7. Расчет индукции магнитного поля в центре и на оси плоского витка на расстоянии Х от его центра.

Литература

1. А. В. Астахов, Ю. М. Широков. Курс физики. М.: «Наука», 1980. Т. II. 359 с.

2. Р. Фейнман, Р. Лейтон, М. Сэндс. Фейнмановские лекции по физике. М.: «Мир», 1966. Вып. 5. 296 с.

3. Д. В. Сивухин. Общий курс физики. Т. III. Электричество. М.: «Наука», 1977. 688 с.

4. И. Е. Иродов. Электромагнетизм. Основные законы. М.-СПб.: Физматлит, 2000. 350 с.

Дата добавления: 2015-10-29